Космическая гантеля

[Ost]

У меня получилась другая формула
\[\Delta x=(R_5-h)(\varphi cos\varphi -sin\varphi )=-0,02191291\]
\[\varphi =\omega t_п=\sqrt{\frac{1}{(1-\frac{h}{R_5})^2}-1}\]
Отклонение от центра пола в сторону противоположную вращению станции.

Угловая скорость тела и станции немного отличаются.

Отклонение от центра пола в сторону противоположную вращению станции.

Да, начальная скорость отрицательна, тело отстаёт.

[Иван Горин]

Угловая скорость тела и станции немного отличаются.Да, начальная скорость отрицательна, тело отстаёт.

Я решаю задачу в ИСО. У тела нет угловой скорости. Оно при отрезании верёвочки движется по касательной к траектории с постоянной скоростью. И эта скорость направлена в сторону вращения станции.
Но горизонтальная составляющая скорости (ИСО) линии потолок-пол опережает тело.
Будет время приведу новый чертёж и вывод формулы.
Но мы должны получить формулу Дробышева.
И что у него принять за R. Радиус до пола этажа или до потолка.
В моей формуле отклонения - отклонение от пола 5 этажа. Сейчас проверю формулу Дробышева.

[Ost]

[Иван Горин]

Я не понимаю этот вывод.
Можно записать:
\[\Delta x=R\sqrt{1-(1-\frac{h}{R})^2}-(R-h)\arccos (1-\frac{h}{R})\]
Как быть дальше?

[Ost]

Я не понимаю этот вывод.
Можно записать:
\[\Delta x=R\sqrt{1-(1-\frac{h}{R})^2}-(R-h)\arccos (1-\frac{h}{R})\]
Как быть дальше?

Просто, пользуясь функцией serits получил два члена ряда и упростил.
В ручном варианте надо получить ряд Лорана или Тейлора.
При попытке разложить в ряд Тейлора, выясняется, что в точке 0 вторая производная равна нулю, а
третья уходит в бесконечность.
Далее не стал разбираться, просто убедился, используя функции программы, что результат сходится к формуле.

[Иван Горин]

У меня получилась другая формула
\[\Delta x=(R_5-h)(\varphi cos\varphi -sin\varphi )=-0,02191291\]
\[\varphi =\omega t_п=\sqrt{\frac{1}{(1-\frac{h}{R_5})^2}-1}\]
Отклонение от центра пола в сторону противоположную вращению станции.

Разлагаю sin и cos в ряд Тейлора и беру два члена разложения.
Получаю формулу:
\[\Delta x=(1-\frac{h}{R_5})\sqrt{\frac{8h^3}{9R_5}}\]
R5 расстояние от центра вращения до пола 5 этажа.
Если я не ошибся в выводе. Величиной второго порядка малости я пренебрёг и также пользовался формулой Тейлора.
\[\frac{1}{1-x}=1+x\]
x величина первого порядка малости.
Интересно сравнить все 4 формулы для станции с радиусом вращения 250 м и потолком 3 м.

[Ost]

[Иван Горин]

Михаил, по оси ординат должно быть отклоенние в см, по оси обсцисс радиус от центра вращения до пола каюты в км. Высота каюты постоянная:  3 метра. И надо привести ещё мою полную формулу. В преобразованиях при разложении в ряд Тейлора я мог сделать ошибку.
Иначе твой график мне непонятен.

[Ost]

[Иван Горин]

Отлично. После 250 м все формулы сходятся. Где-то у нас был проект станции с радиусом 250 м. И этот проект, как видим работает. Можно играть в волейбол.

[Ost]

Отлично. После 250 м все формулы сходятся. Где-то у нас был проект станции с радиусом 250 м. И этот проект, как видим работает. Можно играть в волейбол.

Отклонение в метрах.

[Иван Горин]

Отклонение в метрах.

То есть на станции с радиусом 250 м тело с высоты 3 м отклоняется на полметра?

[Ost]

То есть на станции с радиусом 250 м тело с высоты 3 м отклоняется на полметра?

Примерно 31 см на 250 метрах.

[Иван Горин]

Появились ещё одна идея.
Тело массой m пройдёт расстояние по горизонтали ИСО до встречи с окружностью радиуса R₅:
\( \omega (R_5-h)\omega tп\)
За это время станция повернётся на угол:
\(\varphi _2=\omega t_п\)
В этот момент времени угол между вертикалью и точкой встречи тела с окружностью R₅:
\[\varphi _1=\arctan \frac{\omega (R_5-h)t_п}{R_5-h}=\arctan (\omega t_п)\]

Угол отклонения от вертикали в каюте станции:
\(\Delta \varphi =\varphi _2-\varphi _1\)
Длина дуги отклонения:
\(\Delta L=R_5[ \omega t_п-\arctan (\omega t_п)]\)
\[\arctan x\approx x-\frac{x^3}{3}\]
\[\Delta L=R_5\frac{x^3}{3}\]
время падения находим по теореме Пифагора из моих чертежей
\((R_5-h)\omega t_п=\sqrt{R_5^2-(R_5-h)^2}\)
Откуда находим
\[x=\omega t_p=\sqrt{\frac{1}{(1-\frac{h}{R_5})^2}-1}\approx \sqrt{2\frac{h}{R_5}}\]
\[\Delta L=\frac{R_5}{3}\sqrt{\frac{8h^3}{R_5^3}}=\sqrt{\frac{8h^3}{9R_5}}\]

[Иван Горин]

Просто, пользуясь функцией serits получил два члена ряда и упростил.
В ручном варианте надо получить ряд Лорана или Тейлора.
При попытке разложить в ряд Тейлора, выясняется, что в точке 0 вторая производная равна нулю, а
третья уходит в бесконечность.
Далее не стал разбираться, просто убедился, используя функции программы, что результат сходится к формуле.

Михаил, третья производная от arccos в нуле равна -1
\[\arccos z\approx \frac{\pi }{2}-z-\frac{z^3}{6}\]
\[\arcsin z\approx z+\frac{z^3}{6}\]
Тогда из твоей формулы для отклонения невозможно получить формулу Дробышева.
Твою формулу:
\[\Delta L=Rsin(\arccos \frac{R-h}{h})-(R-h)\arccos \frac{R-h}{h}\]
Можно привести к виду:
\[\Delta L=Rz-(R-h)\arcsin z\]
Где
\[z=\sqrt{1-(1-\frac{h}{R})^2}\approx \sqrt{2\frac{h}{R}}\]


Возможно я ошибся в преобразованиях. Проверь пожалуйста.

[Ost]

Михаил, третья производная от arccos в нуле равна -1
\[\arccos z\approx \frac{\pi }{2}-z-\frac{z^3}{6}\]
\[\arcsin z\approx z+\frac{z^3}{6}\]
Тогда из твоей формулы для отклонения невозможно получить формулу Дробышева.
Твою формулу:
\[\Delta L=Rsin(\arccos \frac{R-h}{h})-(R-h)\arccos \frac{R-h}{h}\]
Можно привести к виду:
\[\Delta L=Rz-(R-h)\arcsin z\]
Где
\[z=\sqrt{1-(1-\frac{h}{R})^2}\approx \sqrt{2\frac{h}{R}}\]


Возможно я ошибся в преобразованиях. Проверь пожалуйста.

\(z=\sqrt{1-(1-\frac{h}{R})^2}\approx \sqrt{2\frac{h}{R}}\) - в этом приближении потерян второй член ряда.

\((R-h)~arcsin~z\) - здесь необходимо учесть третий член ряда.

[Иван Горин]

\(z=\sqrt{1-(1-\frac{h}{R})^2}\approx \sqrt{2\frac{h}{R}}\) - в этом приближении потерян второй член ряда.

\((R-h)~arcsin~z\) - здесь необходимо учесть третий член ряда.

Возможно так.
Можешь привести полные выкладки, чтобы из твоей формулы получить формулу Дробышева.
Я для своей новой формулы такие выкладки привёл.
Возможно ты это не заметил.

[Ost]

Возможно так.
Можешь привести полные выкладки, чтобы из твоей формулы получить формулу Дробышева.
Я для своей новой формулы такие выкладки привёл.
Возможно ты это не заметил.

Возможно так.

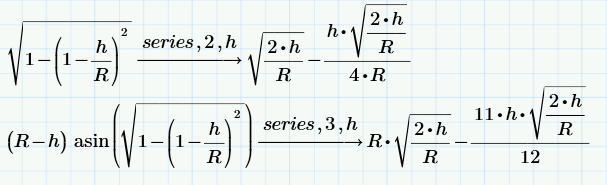
Функция series, вычисляет члены ряда Тейлора или Лорана. Первый параметр, число членов.
Второй, переменная по которой происходит построение ряда.

Можешь привести полные выкладки, чтобы из твоей формулы получить формулу Дробышева.

Нет ручных выкладок, только результат работы функций программы.

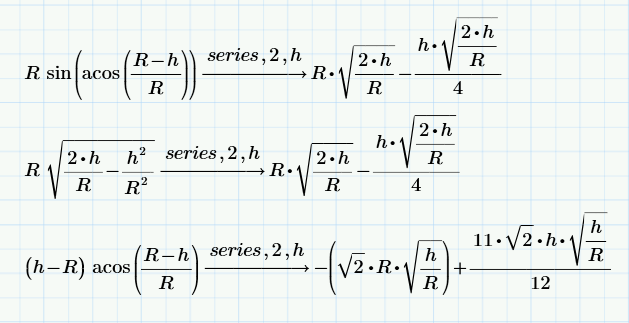
Я для своей новой формулы такие выкладки привёл.
Возможно ты это не заметил.

Такой вариант математически не строгий, невозможно контролировать потерю точности в таких приблизительных преобразованиях.
Это видно на примере функции
\(\Delta L=R~z - (R-h)\arcsin z\).
Где требуется учёт третьего члена ряда для получения правильного результата.

[Иван Горин]

Отличная у тебя программа, Михаил.
Только так раскладывает в ряды.
А у меня действительно была ошибка.
Надо было сделать сначала все преобразования, и только в конце пренебречь малыми второго порядка.
Но в моей формуле с арктангенсом ошибки нет.
И к тебе вопрос.
Твоя формула для отклонения на полу или потолке станции?

[Ost]

Отличная у тебя программа, Михаил.
Только так раскладывает в ряды.
А у меня действительно была ошибка.
Надо было сделать сначала все преобразования, и только в конце пренебречь малыми второго порядка.
Но в моей формуле с арктангенсом ошибки нет.
И к тебе вопрос.
Твоя формула для отклонения на полу или потолке станции?

Относительно пола.
Выводится из \(\displaystyle h=-R_0~e^{i\Omega_z t} + i~(\Omega_z (R_0 - h_0)+v_0)~t + (R_0-h_0)\).