Космическая гантеля

[Ost]

Это понятно. Но как же быть с ускорением Кориолиса?

Ускорение Кориолиса это просто функция \(\displaystyle -i 2 \Omega_z~v(t)\)
Ускорение полученное дифференцированием результата решения

не обязано содержать ускорение Кориолиса в явном виде.
Оно просто должно удовлетворять исходному уравнению.

 

[Иван Горин]

Ускорение Кориолиса это просто функция \(\displaystyle -i 2 \Omega_z~v(t)\)
Ускорение полученное дифференцированием результата решения

не обязано содержать ускорение Кориолиса в явном виде.
Оно просто должно удовлетворять исходному уравнению.

 

В ускорении, которое мы нашли нет в явном виде ни ЦБ ускорения, ни ускорения Кориолиса.
Но я их нашёл.
К нашим ускорениям надо прибавить и отнять слагаемое с i.
И всё получим в явном виде.
Задача решена.
Теперь твоя задача:

На пятом этаже корабля поднимают груз со скоростью 1 м/c.
Найти угол отклонения троса от вертикали.
Записать закон сохранения энергии с учётом вращения корабля.

Лебёдка закреплена на потолке.
Груз движется в поле сил инерции и на него действует сила реакции со стороны троса.

[Ost]

В ускорении, которое мы нашли нет в явном виде ни ЦБ ускорения, ни ускорения Кориолиса.
Но я их нашёл.
К нашим ускорениям надо прибавить и отнять слагаемое с i.
И всё получим в явном виде.
Задача решена.
Теперь твоя задача:

На пятом этаже корабля поднимают груз со скоростью 1 м/c.
Найти угол отклонения троса от вертикали.
Записать закон сохранения энергии с учётом вращения корабля.

Лебёдка закреплена на потолке.
Груз движется в поле сил инерции и на него действует сила реакции со стороны троса.

Уравнение можно записать так
\(\displaystyle m~ \vec a =\vec f -2m \left[\vec \Omega_z \times \vec v \right] + m~Ω_z^2~ \vec r\), где \(\vec f~-\) сила реакции со стороны троса.

[Ost]

Направление \(\vec f\) и \(\vec r\) не совпадает, просто исключить член нельзя.
Можно его записать как постоянный и приблизительно решить задачу в статическом варианте.
\(\displaystyle \vec f -2m \left[\vec \Omega_z \times \vec v \right] + m~Ω_z^2~ \vec R = 0\).

[Ost]

Координаты в каюте.
x направим вправо от потолка по горизонтали- мнимая ось.
y направим от потолка к полу - действительная ось.

Лучше y мнимая по горизонтали, как в предыдущей задаче.

Скорость с которой опускаем груз на верёвке это радиальная составляющая, направлена по оси y.

Лучше по вектору троса. Реально он удлиняется.

Если по уравнению \(\displaystyle \vec f -2m \left[\vec \Omega_z \times \vec v \right] + m~Ω_z^2~ \vec R = 0\), то
движение будет с постоянной скоростью.

\(h(t)=v_0 t (cos(\alpha) + i~sin(\alpha))\), где \(\alpha\) постоянный угол между тросом и вертикалью.
Угол определяется из условия равновесия сил.

Если по уравнению \(\displaystyle m~ \vec a =\vec f -2m \left[\vec \Omega_z \times \vec v \right] + m~Ω_z^2~ \vec r\), всё будет значительно сложнее.
Надо вычислять \(\vec f\), который зависит от сил инерции.
Это отдельная важная задача. 

[Ost]

Трос с блоком крепится на потолке лаборатории. Груз просто поднимается лебёдкой.
Уравнение по определение записано неверно, так как не содержит полного набора сил инерции (центробежная+Кориолиса).
Всё определяется по уравнению \(\displaystyle m~ \vec a =\vec f -2m \left[\vec \Omega_z \times \vec v \right] + m~Ω_z^2~ \vec r\)
его нельзя обойти без риска ошибиться.

Необходимо правильно учесть кинематику троса.
Она влияет на распределение сил, формирует ускорения.
Надо записать дополнительное уравнение следующее из кинематики троса
в векторном виде.

[Ost]

Силу реакции можно записать так
\(\vec f(\vec r)=-m~ \vec q(\vec r) \cdot (\vec q(\vec r) \cdot \vec a)\), где \(\vec q~ - \) единичный вектор вдоль троса.

[Ost]

Задача.
На пятом этаже корабля поднимают груз со скоростью 1 м/c.
Найти угол отклонения троса от вертикали.
Записать закон сохранения энергии с учётом вращения корабля.

Лебёдка закреплена на потолке.
Груз движется в поле сил инерции и на него действует сила реакции со стороны троса.

[Иван Горин]

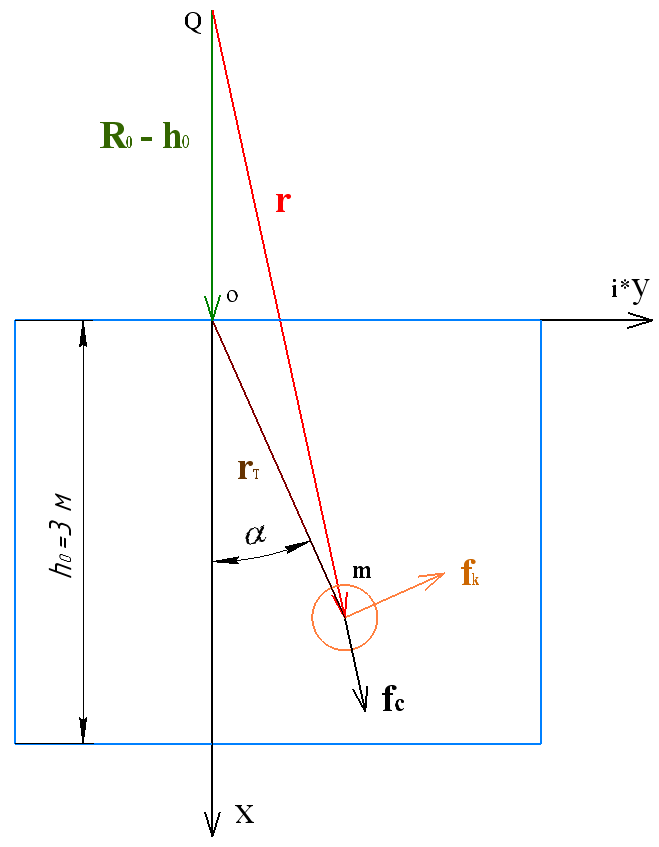
Отличный чертёж.
Из него видно, что сила Кориолиса перпендикулярна радиус вектору \(\bar{r_\tau}\) и следовательно вектору скорости.
Это может быть в том и только в том случае, когда угол \(\alpha =const\)
Докажем это
\(\bar{r_\tau }=Vte^{i\alpha }\)
\[\dot{\bar{r_\tau }}=Ve^{i\alpha }\]
\[\bar{f_k}=2im\omega Ve^{i\alpha }\]
Делаем проверку. Может ли быть угол \(\alpha =const\)
За врямя t груз пройдёт по радиусу \(\bar{r_\tau}\) расстояние Vt
За это же время под действием постоянной силы Кориолиса груз пройдёт расстояние по перпендикуляру к этому вектору
\[2\omega V\frac{t^2}{2}=\omega Vt^2\]
\[\alpha =\arctan \frac{\omega Vt^2}{Vt}=\arctan \omega t\neq const\]

Это было доказательство методом от противного.
И это не значит, что улол \(\alpha =\arctan \omega t\)

Продолжение следует...

[Иван Горин]

Сила, действующая на груз в свободном движении
\[\bar{F}=\bar{F}_{ЦБ}+\bar{F}_k=m\omega ^2\bar{r}-2im\omega \dot{\bar{r }}\]
На груз также действует сила натяжения троса \(\bar{F_\tau}\).
Эта сила направлена от груза к потолку и противоположна вектору \(\bar{r_\tau}\)
\[F_\tau=Fcos(\alpha -arg(\bar{F}))\]
\[\bar{F_\tau}=-F_\tau\frac{\bar{r_\tau }}{r_\tau }\]
Подставляем найденную силу реакции троса в наше дифур
\[\ddot{\bar{r}}+2i\omega \dot{\bar{r}}-\omega ^2\bar{r}=\bar{F_\tau}\]
Учтём, что \(\bar{r}=\bar{r_\tau} +(R-h)\)

\[\ddot{\bar{r_\tau }}+2i\omega \dot{\bar{r_\tau }}-\omega ^2(\bar{r_\tau} +(R-h))=\bar{F_\tau}\]

[Ost]

Сила, действующая на груз в свободном движении
\[\bar{F}=\bar{F}_{ЦБ}+\bar{F}_k=m\omega ^2\bar{r}-2im\omega \dot{\bar{r }}\]
На груз также действует сила натяжения троса \(\bar{F_\tau}\).
Эта сила направлена от груза к потолку и противоположна вектору \(\bar{r_\tau}\)
\[F_\tau=Fcos(\alpha -arg(\bar{F}))\]
\[\bar{F_\tau}=-F_\tau\frac{\bar{r_\tau }}{r_\tau }\]
Подставляем найденную силу реакции троса в наше дифур
\[\ddot{\bar{r}}+2i\omega \dot{\bar{r}}-\omega ^2\bar{r}=\bar{F_\tau}\]
Учтём, что \(\bar{r}=\bar{r_\tau} +(R-h)\)

\[\ddot{\bar{r_\tau }}+2i\omega \dot{\bar{r_\tau }}-\omega ^2(\bar{r_\tau} +(R-h))=\bar{F_\tau}\]

Противоречий не обнаружил, но это сложный путь и надо исключить \(\alpha\).

[Иван Горин]

Противоречий не обнаружил, но это сложный путь и надо исключить \(\alpha\).

Да, решение в аналитическом виде очень сложное.
Разность углов можно исключить. Но это огромные тригонометрические преобразования.
И после таких преобразований решение нашего дифур будет очень сложным в аналитическом виде.
Не зря я в начале сказал,  что эта задача гораздо сложнее, чем свободное движение тела при обрезании верёвки у потолка.
А возможно есть более простой путь без упрощений.
Надо Дробышева попросить для помощи. Он в таких задачах спец.

[Ost]

Да, решение в аналитическом виде очень сложное.
Разность углов можно исключить. Но это огромные тригонометрические преобразования.
И после таких преобразований решение нашего дифур будет очень сложным в аналитическом виде.
Не зря я в начале сказал,  что эта задача гораздо сложнее, чем свободное движение тела при обрезании верёвки у потолка.
А возможно есть более простой путь без упрощений.
Надо Дробышева попросить для помощи. Он в таких задачах спец.

Можно непосредственно выделить ускорение кинематически возможное в этой схеме
\(\displaystyle \vec a=\vec Q(\vec r) \cdot \left(\vec Q(\vec r) \cdot \left(-2 \left[\vec \Omega_z \times \vec v \right] + Ω_z^2~ \vec r \right) \right)\), где \(\vec Q(\vec r)~-\) единичный
вектор перпендикулярный тросу, из центра масс груза.

[Иван Горин]

Можно непосредственно выделить ускорение кинематически возможное в этой схеме
\(\displaystyle \vec a=\vec Q(\vec r) \cdot \left(\vec Q(\vec r) \cdot \left(-2 \left[\vec \Omega_z \times \vec v \right] + Ω_z^2~ \vec r \right) \right)\), где \(\vec Q(\vec r)~-\) единичный
вектор перпендикулярный тросу, из центра масс груза.

Какое конечное дифф. ур. мы получим в этом случае?

[Ost]

Какое конечное дифф. ур. мы получим в этом случае?

\(\displaystyle \vec a=\vec Q(\vec r) \cdot f\left(\vec r, \vec v \right)\).
Вектор как функция координат со скалярным множителем зависимым от координат и скорости.
Будет проще.
\(\displaystyle \vec Q(\vec r_\tau) = \frac{\left[\vec \Omega_z  \times \vec r_\tau \right]}{|\vec \Omega_z| \cdot |\vec r_\tau|}\).

\(\displaystyle \vec a_\tau = \frac{\left[\vec \Omega_z  \times \vec r_\tau \right]}{|\vec \Omega_z| \cdot |\vec r_\tau|} \cdot \left(\frac{\left[\vec \Omega_z  \times \vec r_\tau \right]}{|\vec \Omega_z| \cdot |\vec r_\tau|} \cdot \left(-2 \left[\vec \Omega_z \times \vec v_\tau \right] + Ω_z^2~ (\vec r_\tau+ \vec r_0) \right) \right)  \).

[Иван Горин]

\(\displaystyle \vec a=\vec Q(\vec r) \cdot f\left(\vec r, \vec v \right)\).
Вектор как функция координат со скалярным множителем зависимым от координат и скорости.
Будет проще.
\(\displaystyle \vec Q(\vec r_\tau) = \frac{\left[\vec \Omega_z  \times \vec r_\tau \right]}{|\vec \Omega_z| \cdot |\vec r_\tau|}\).

\(\displaystyle \vec a_\tau = \frac{\left[\vec \Omega_z  \times \vec r_\tau \right]}{|\vec \Omega_z| \cdot |\vec r_\tau|} \cdot \left(\frac{\left[\vec \Omega_z  \times \vec r_\tau \right]}{|\vec \Omega_z| \cdot |\vec r_\tau|} \cdot \left(-2 \left[\vec \Omega_z \times \vec v_\tau \right] + Ω_z^2~ (\vec r_\tau+ \vec r_0) \right) \right)  \).

То есть вектор силы в свободном движении поворачиваем на 90° относительно вектора троса и получаем ускорение груза, соединённого с тросом.
Не понятно почему так.
Пока я отвечал ты кое что добивил.
Единичный вектор в квадрате даёт в механике единицу. Или нет?

[Ost]

То есть вектор силы в свободном движении поворачиваем на 90° относительно вектора троса и получаем ускорение груза, соединённого с тросом.
Не понятно почему так.

Находим проекцию вектора ускорения в свободном движении на направление движения определённое кинематикой.

Да, единичный вектор в квадрате даёт единицу.

[Иван Горин]

Находим проекцию вектора ускорения в свободном движении на направление движения определённое кинематикой.

Да, единичный вектор в квадрате даёт единицу.

Но в твоей формуле для а тау есть единичный вектор в квадрате.

[Ost]

Но в твоей формуле для а тау есть единичный вектор в квадрате.

То, что в скобках даёт проекцию.
Единичный вектор за скобками даёт направление.
Сначала производится скалярное умножение, а затем умножение на единичный вектор.

[Иван Горин]

То, что в скобках даёт проекцию.
Единичный вектор за скобками даёт направление.
Сначала производится скалярное умножение, а затем умножение на единичный вектор.

Да, получается.
Остаётся решить дифф. ур.