Структура волновых полей ч. 1 Продольные волны

[Иван Горин]

Тема опять открыта.
Прошу участников воздержаться от взаимных оскорблений и переходов на личности.
zero43 в этом подразделе "Физика и математика" забанен.

[Семенец Ю.Л.]

                                                                                      Продольные волны:

[sergey_B_K]

                                                                                      Продольные волны:

Если честно, мне постоянно жаль сторонников структуризации эфира. Тем более, в стиле матрёшки. Огромные "свирепые" формулы, необъятные согласования, но что в результате?
С начала же...
- масса определяется через единичный заряд. Но это заряды должны, с одной стороны, отталкивать друг друга, с другой стороны,  как они сформируют заряд электрона на следующем уровне иерархии?
- структура состоит из электрония и позитрония. Это, что-то из разряда Бульона Дирака, но структурированное. Но это неустойчивая структура. Атом устойчив потому, что электроны значительно легче и обязательно вращаются вокруг ядра. Этим и обусловлены как стабильность, так и взаимодействие с другими атомами. А тут? Тоже вращаются? Но при равных массах это будет совсем иная структура, чем показано.
- Электроний и позитроний взаимодействуют чтобы образовать структуру? А как? Матрёшка? Но ведь это не решение задачи. В такой системе скорость распространения волн будет определяться свойствами тех полей, которые в следующей подматрёшке. А каковы её свойства? Опять-таки, скорость распространения волн будет, как в веществе, т.е. частично определяться структурой, а частично свойствами самого эфира, но формулу Максвелла для скорости света откровенно не получим... и волновое сопротивление тоже...
- далее, любое кристаллическое тело обладает анизотропией распространения волн по направлениям. Это неизбежно. Значит, и здесь будет анизотропия?
- далее, в этой структуре, что представляют собой электрон и протон, не говоря о других частицах?
Ну, и далее, далее, далее. Я хочу чтобы правильно меня поняли. У меня нет каких-либо намерений рубить с плеча. Заданные мной вопросы, как и все последующие, стандартны для множества попыток описать эфир хоть твёрдым телом, хоть жидкостью, хоть газом.
Тут иначе стоит вопрос. Вот Вы написали кучу формул, внеся туда всё, что можно и нельзя из вышестоящего уровня. Например, та же постоянная Планка, в действительности, представляет собой совсем иное, чем ей приписывают, а уж закон полной энергии относится к релятивистским скоростям и вообще некорректный. Исходно у Томсона он представлял собой энергию внешнего поля, а не то, что сделали из него релятивисты.
Так вот. Совпадениями цифр здесь ничего не доказывается. Что может предложить автор для строгого экспериментального физического доказательства своей структуры? То, что отличало бы именно эту структуру от всех остальных попыток и демонстрировало её наличие?

[Семенец Ю.Л.]

Если честно, мне постоянно жаль сторонников структуризации эфира.

Вариантов то два, либо космическое пространство, либо геометрическое пространство.

То что существует космическое пространство с физическими характеристиками вещества диэлектрика (проницаемости, волновое сопротивление, скорость распространения волны, температура) достоверно известно. А существует ли придуманный геометрический образ пустого пространства без физических характеристик?  Это гипотеза.


Мне вас тоже  (всех) жаль,  так как вы  неспособны отличать придуманные вами образы от материи, образы от  материальных объектов, и не только речь о пространстве. 

Официально полем называется область пространства, в каждой точке которой действует сила, на помещённое в эту точку тело/заряд.

Сила – образ (инструмент, параметрическая функция), образ на объект действовать не может. На материальный объект может действовать только материальный объект.
 Функция "Заряд" тоже функция, как и энергия с работой.
Работу ввели только для того чтобы прикрыть дыры,  с точки зрения принятой модели вокруг все состоит из вечных двигателей, работа их и прикрывает.

Функция заряд покалечила понятый сознанию механический инструмент (механические законы).
Адекватное моделирование возможно только понятным сознанию механическим инструментом.
Законы электромагнетизма описывают микромир, если удалить из них функцию «заряд», то они перейдут в механические законы,  из которых вытекает модель структуры микромира и происходящие процессы.



Заряд легко удаляется из всех законов:



Многократно показывал решения задач из разных областей физики, структура везде работает нормально, таких совпадений не бывает.

Удалите заряд,   и все встанет на свои места. Там  где не сможете, я Вам помогу.
Можем, без заряда, (механическим инструментом) порешать, в том числе, задачи с использованием уравнений Максвелла. 


«Матрешка»  здесь еще не затрагивалась.

Есть главный закон для любой вселенной (если они есть),

для нашей:



из которого вытекают все главные известные законы, в том числе постоянные Бора, Ридберга, ...



И много неизвестных ранее, в том числе закон ускоренного распространения гравитации:

http://bolshoyforum.com/forum/index.php?topic=533109.0



 

Что может предложить автор для строгого экспериментального физического доказательства своей структуры?

Все уже обнаружено, измерено и доказано,  только надо это увидеть, а для этого надо вывести из законов электромагнетизма функцию «заряд».

Вопросов Вы задали очень много.  На них у меня есть ответы, но это будет уводить в разные стороны от  «гнезда».  Если пойдете по верному (кратчайшему) пути, то большинство вопросов отпадут.

[в.макаров]

Ну, это же не ответы, уважаемый макаров. Так можно отмахнуть ручкой на всё, что угодно...
Так значит
Цитировать
Объяснять наличие частоты у фотона возможно при доказанности наличии этой частоты.
Значит, частота не доказана? А формула Планка?

Она не для корпускул? 
Также и с интерференцией. Значит,
Цитировать
Утверждение в вопросе об интерференции (сложении волн) частиц света не имеет основания.
Но это свойство света. Нет объяснения интерференции и дифракции, нет и корпускулярной концепции, как ни пытайся "трактовать"... 
Наконец, о спине фотона.
Цитировать
Естественно, речь не идёт о предполагаемом спине фотона, его частоте
Так значит, нет плоско поляризованного луча, призм Френеля. И всё потому, что понимаете ли, фотонщикам это неудобно. Так о чём говорить? Сначала нужно быть честными в суждениях, а потом уже спрашивать что дальше... 

Мои ответы вы за ответы не принимаете. После анализа ваших постов, полагаю, что нашёл причину вашего неприятия. Причина простая — мои ответы не соответствуют вашему представлению о свете. Действительно, для лучшего понимания друг друга всегда полезно оговорить начальные условия и термины.
Мы обсуждаем понимание света. Вы, придерживаясь классической физики, допускаете рассматривать свет как фотоны (частицы). Тут у нас нет разногласия. Разногласие в определении или представлении о фотоне. Если я вас правильно понял, то ваши представление о фотоне соответствуют представлению Планка. Как нечто ограниченное, описываемого колебательным процессом. Частота колебаний соответствует частоте рассматриваемого света и отражённая в формуле Планка для определения энергии кванта. Потому и используете волновую терминологию и критику такой терминологии не допускаете. Как заметил МЕАНДР: «Последовательной волновой теории света как электромагнитно-полевого явления (да еще и в рамках классических представлений о пространстве и времени) я у Вас к сожалению не нахожу, не говоря об экспериментальных доказательствах того, что В РЕАЛЬНОСТИ будет ИМЕННО ТАК». Т.е. принятое вами представление о фотоне принимаете как догму, не подвергаемую сомнению. Это представление ранее считалось принятым научным сообществом, описывалось в учебниках и популярной литературе. Похоже, вы застряли в прошлом. В настоящее время свет принято считать как корпускулы (фотоны), а волновые свойства относят к вероятности распределения фотонов в интерференционных картинах. При таком представлении о свете возможно дальнейшее обсуждение. При вашем варианте представления обсуждение не может быть продуктивным. Тем более, приложение понимания света как частица-волна к объяснению реальных опытов со светом вы можете только декларировать.

[в.макаров]

 
Много букафф и нудно, но в целом на 100% верно, если перестать думать о частицах, фотоне и прочих атрибутов давно ушедшего времени.

Если не думать о  частицах и фотонах, то какой парадигме света вы придерживаетесь?

[в.макаров]

Я начал копать в учебниках, как и откуда берется свет.
Копания привели меня к электрону, как он, при получении энергии извне, постепенно, скачками переходит на самый верхний, неустойчивый уровень, а потом, по пока неизвестной причине, взрывается квантом энергии и падает на нижний уровень. И так циклически постоянно.
Это описано во многих учебниках. 
Теперь уже известно, что нет электрона, а есть электронное облако и становиться понятным, что и дуализма нет - дуалисты исходили из предположения твердого электрона... 
А дальше - больше.
Если интересно - расскажу...

В учебниках излучение связывают с изменением положения электрона в атоме. Но есть синхротронное излучение, в котором объяснение излучения связывают с самим электроном. Есть ли у вас свой вариант объяснения излучения?

[в.макаров]

Что-то не попадалось таких учебников... 
Слово "орбитали" ничего не говорит?

Допускаю, что вы не видели этих учебников. Но орбитали чего и вокруг чего?

[в.макаров]

Я не четко поставил вопрос? -  Слово "орбитали" ничего не говорит? 

Само слово "орбиталь" без связи с другими словами ничего не "говорит". Если будете использовать не связанные друг с другом слова, то кто же вас поймёт?

[Rishi]

Если честно, мне постоянно жаль сторонников структуризации эфира.

давайте и не будем структурировать, а считать эфир просто непрерывной физической средой. И вернёмся всё-таки к названию темы.
Так что такое по-вашему продольные волны?  Дайте определение, пожалуйста. И как они формируются в свободном эфире под действием движущегося заряда? Что нужно исправить в уравнениях  Максвелла, чтобы  появились эти продольные волны?
И  расскажите кратко про ваши эксперименты по обнаружению продольных волн. 

[sergey_B_K]

давайте и не будем структурировать, а считать эфир просто непрерывной физической средой. И вернёмся всё-таки к названию темы.
Так что такое по-вашему продольные волны?  Дайте определение, пожалуйста. И как они формируются в свободном эфире под действием движущегося заряда? Что нужно исправить в уравнениях  Максвелла, чтобы  появились эти продольные волны?
И  расскажите кратко про ваши эксперименты по обнаружению продольных волн.

Прежде всего, я рад, что, наконец-то, приходят к тому, что пока в структуру эфира рано лезть. Дел хватает и на том уровне, на котором эфир представляется некоей материальной субстанцией с некоторыми известными нам свойствами, обеспечивающими распространение силовых полей и волн. О физике этого процесса говорить рано.
Продольные волны являются возмущением субстанции вы направлении своего распространения, в отличие от поперечных, в которых смещение происходит в направлении, перпендикулярном распространению.
В принципе, продольные волны порождают поперечные и наоборот. Вот, в частности, как два изменяющихся во времени заряда, поля каждого из которых  продольные, создают поперечную волну:

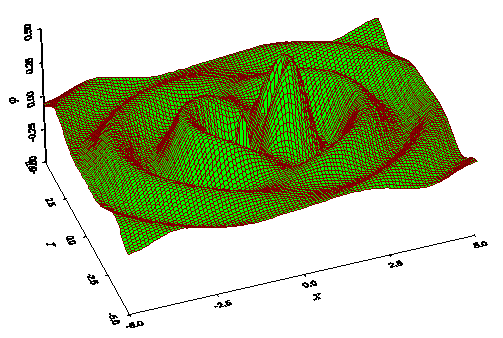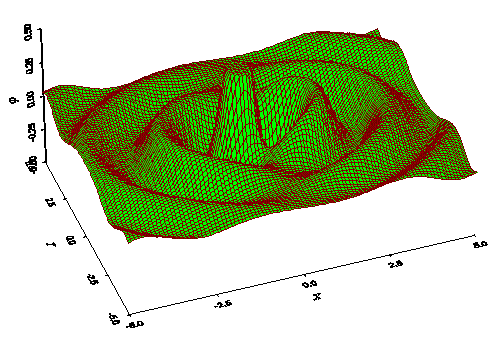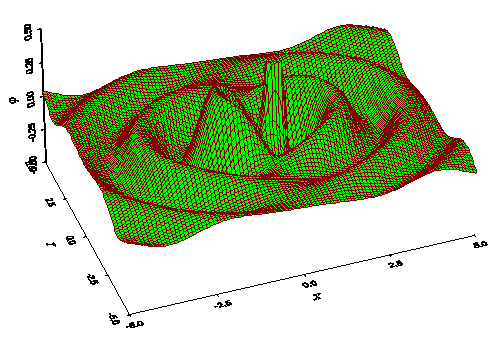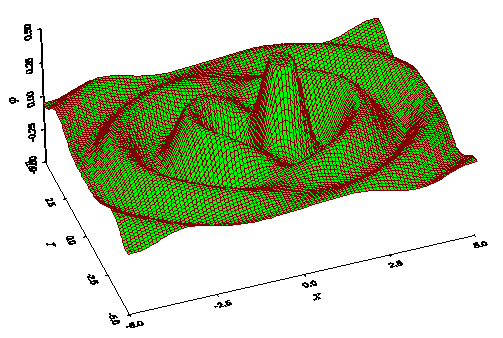http://selftrans.narod.ru/v4_1/dipole/d20/drus20.html
Поперечные тоже в локальной области могут создавать продольные, но эти области слишком малы, чтобы с их помощью пытаться возбуждать продольные волны.
ЭМ волна ещё более сложное образование. Там играет роль и поле индуцирующих токов, без которого не будет ни продольной, ни поперечной волны в дальней зоне.
Так, в частности, когда мы проводили эксперименты с возбуждением поперечной акустической волны
"ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ И ЭКСПЕРИМЕНТАЛЬНОЕ ПОДТВЕРЖДЕНИЕ СУЩЕСТВОВАНИЯ ПОПЕРЕЧНОЙ АКУСТИЧЕСКОЙ ВОЛНЫ В ГАЗЕ"
http://selftrans.narod.ru/v2_1/acoustics/acoustics03/acoustics3rus.html
то все наши попытки реализовать дипольных вариант были безуспешными. Заработал только аналог полуволнового вибратора

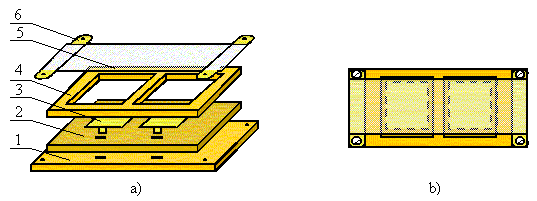
хотя для объяснения самого принципа формирования поперечных волн мы использовали дипольную схему, как более простую и наглядную.

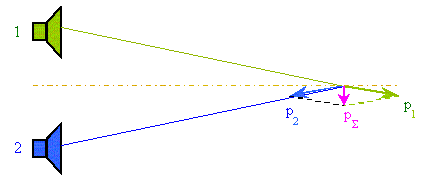
Это если очень коротко, поскольку сам вопрос обширен.
Теперь по поводу изменений в уравнениях Максвелла. То, что я сделал - это далеко не до конца, но система уравнений начинает видеть продольные волны если перейти от законов сохранения (дивергенция вектора) для статических полей, заложенных в существующие уравнения, к закону сохранения в динамических полях. Теорема была представлена АН СССР ещё в 1985 году и благополучно зарублена. Доложена на международной конференции в Рустави в 1991 году. Удалось её опубликовать в международном журнале только в 2001 году
Karavashkin, S.B. Transformation of divergence theorem in dynamic fields. Archivum Mathematicum, 37 (2001), 3, 233 – 243 русский текст
http://selftrans.narod.ru/archive/div/divergence/div1/div1rus.html
Особенность в том, что в динамических полях правая честь закона сохранения в области без источников и стоков - не нулевая, а имеет вид

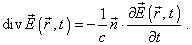
Это волновое уравнение первой степени, которое и определяет волны. Да, оно скалярное, но это не означает появление неких мифических скалярных силовых полей, как долгое время мучаются многие. Скалярность только определяет тот факт, что у продольной волны нет поляризации. Поперечная волна поляризована и потому закон сохранения для неё имеет вид

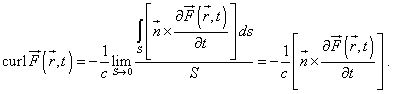
О.Н. Каравашкина, С.Б. Каравашкин Теорема о роторе потенциального вектора в динамических полях
http://selftrans.narod.ru/v2_2/curl/curl06/curl06rus.html
а не просто по экспериментам Фарадея и для симметричности, как это было у Максвелла. Индукционная пара уравнений - это тоже законы сохранения.
Вот, если очень коротко. А далее технологии. Там есть свои нюансы, которые несмотря на всю активность, так и не смогли повторить с 1990 г. И без меня ещё долго не смогут... 

[Семенец Ю.Л.]

давайте и не будем структурировать, а считать эфир просто непрерывной физической средой. И вернёмся всё-таки к названию темы.
Так что такое по-вашему продольные волны?  Дайте определение, пожалуйста. И как они формируются в свободном эфире под действием движущегося заряда? Что нужно исправить в уравнениях  Максвелла, чтобы  появились эти продольные волны?
И  расскажите кратко про ваши эксперименты по обнаружению продольных волн.

Что нужно исправить в уравнениях  Максвелла, чтобы  появились эти продольные волны?

                            Забыть про них надо и пользоваться понятными сознанию механическими моделями.

« Ответ #101 : 11 Октябрь 2019, 22:42:42 »


                                              продолжение  задачи к вопросу об уравнениях Максвелла

[sergey_B_K]

Вы, придерживаясь классической физики, допускаете рассматривать свет как фотоны (частицы). Тут у нас нет разногласия. Разногласие в определении или представлении о фотоне. Если я вас правильно понял, то ваши представление о фотоне соответствуют представлению Планка. Как нечто ограниченное, описываемого колебательным процессом.

Извините, но сразу остановлю Вас. Классическая физика ещё в середине 19 века окончательно угла от корпускул Ньютона и перешла на волновую концепцию Гюйгенса. Так что фотонная концепция - это ревизионистская концепция и есчли Вы её сторонник (в любой форме), Вам придётся отвечать на длинную вереницу очень неудобных вопросов, ни на один из которых ни один фотонщик ещё не дал внятного ответа. И никогда не даст.
Если хотите знать моё представление, ознакомьтесь, пожалуйста, с этой работой
Проблемы волновой концепции де Бройля
http://sbkaravashkin.blogspot.com/2016/05/blog-post_20.html
и с этой
С.Б. Каравашкин, О.Н. Каравашкина Легенды волновой механики
http://sbkaravashkin.blogspot.com/2017/05/blog-post_13.html
Много, но тогда будете иметь представление... 

[в.макаров]

Извините, но сразу остановлю Вас. Классическая физика ещё в середине 19 века окончательно угла от корпускул Ньютона и перешла на волновую концепцию Гюйгенса. Так что фотонная концепция - это ревизионистская концепция и есчли Вы её сторонник (в любой форме), Вам придётся отвечать на длинную вереницу очень неудобных вопросов, ни на один из которых ни один фотонщик ещё не дал внятного ответа. И никогда не даст.
Если хотите знать моё представление, ознакомьтесь, пожалуйста, с этой работой

Извините, но я остановлюсь не сразу.
О корпускулярном свете. Считаете, что классическая физика окончательно отошла от корпускулярной концепции к волновой. Это "окончательное" относится с утверждения Томаса Юнга до опытов, показывающих корпускулярные свойства света. К середине прошлого века физика официально признала свет как корпускулы. (см. Мессенджеровские лекции Р. Фейнмана. Лекция №6) Подобно вам можно сказать, что классическая физика окончательно ушла от волновой концепции света.
Полагаю, что утверждения и заданные друг другу вопросы должны показать справедливость каждого. Естественно, обосновывать свои утверждения опытными наблюдениями. Если согласны - задавайте свои вопросы и утверждения.

[sergey_B_K]

Полагаю, что утверждения и заданные друг другу вопросы должны показать справедливость каждого. Естественно, обосновывать свои утверждения опытными наблюдениями. Если согласны - задавайте свои вопросы и утверждения.

Я думаю, Вы посмотрели мои ссылки, чтобы разговор был предметным. Но прежде чем начать разговор, думаю, нужно определиться: будем ли мы опираться на стандартную концепцию фотона или на Ваши или чьи-то вариации? Это важно, поскольку вариации ещё более необоснованны, чем базовая корпускулярная концепция, поскольку не учитывают, что пытаясь замазать одни пробои фотонной концепции, они рвут саму концепцию ещё больше. Итак, будем говорить о базовой концепции фотона? 

[в.макаров]

Я думаю, Вы посмотрели мои ссылки, чтобы разговор был предметным. Но прежде чем начать разговор, думаю, нужно определиться: будем ли мы опираться на стандартную концепцию фотона или на Ваши или чьи-то вариации? Это важно, поскольку вариации ещё более необоснованны, чем базовая корпускулярная концепция, поскольку не учитывают, что пытаясь замазать одни пробои фотонной концепции, они рвут саму концепцию ещё больше. Итак, будем говорить о базовой концепции фотона? 

Для нашей темы, по моему мнению, суть вы выразили: "Ведь не только это отличает частицы и волны. Во-первых, волны подчиняются принципу суперпозиции, т.е. при наложении они складываются, но не взаимодействуют друг с другом, как частицы и, тем более, не передают импульс. Частицы передают друг другу импульс и изменяют свои траектории. Во-вторых, заряженные частицы отклоняются в электрическом и магнитном полях, в то время, как волны, хотя тоже обладают Е и Н- компонентами, внешними полями не отклоняются. В-третьих, волны имеют т.н. время и длину когерентности, т.е. время и протяжённость в пространстве, на котором они не имеют фазовых срывов, да и само понятие фазы присуще именно волне, но не частице. Поток частиц этими свойствами не обладает. Но именно эти свойства позволяют свести без всяких щелей два луча света и в пределах длины когерентности получить интерференционную картину. С частицами это осуществить невозможно ни при каких условиях. Дифракция же электронов, как мы показали в нашей работе[5], обусловлена взаимодействием с динамическими полями атомов структуры, через которую проходят электроны, а не волновыми свойствами самих электронов."
Представление о фотоне. Меня вполне устраивает определение из Вики: "Современная наука рассматривает фотон как фундаментальную элементарную частицу, не обладающую строением и размерами." О этой частице мы судим по её проявлению, т.е. по её свойствам. Вы взяли на себя смелость сделать утверждение, что интерференционную картину частицы не могут создать "ни при каких условиях". Надеюсь, найдёте ответы на мои вопросы о необоснованности рассмотрения света как волны Е и Н полей. А я постараюсь ответить на ваши вопросы.

[sergey_B_K]

элементарную частицу, не обладающую строением и размерами."

Если Вы придерживаетесь базовой концепции фотона, то Вы же понимаете, что вопросов будет вагон и маленькая тележка.
Начнём с простого. Думаю, Вы пробовали получить интерференционную картину от двух обычных фонариков. Как минимум, Вы понимаете, что получить невозможно. Вот теперь представим поток невзаимодействующих фотонов, каждый из которых излучён своим атомом. Что будет в среднем? Будут максимумы/минимумы? В этом описании - никогда. А если мы свет одного источника разделим пополам и сведём, то получим эти полосы. Фотон же, как известно, не делим, тем более, если точечный. Волновая концепция нормально описывает это явление.
Ваше опровержение? 

[в.макаров]

Если Вы придерживаетесь базовой концепции фотона, то Вы же понимаете, что вопросов будет вагон и маленькая тележка.
Начнём с простого. Думаю, Вы пробовали получить интерференционную картину от двух обычных фонариков. Как минимум, Вы понимаете, что получить невозможно. Вот теперь представим поток невзаимодействующих фотонов, каждый из которых излучён своим атомом. Что будет в среднем? Будут максимумы/минимумы? В этом описании - никогда. А если мы свет одного источника разделим пополам и сведём, то получим эти полосы. Фотон же, как известно, не делим, тем более, если точечный. Волновая концепция нормально описывает это явление.
Ваше опровержение? 

О вопросах. В ваших вопросах содержаться утверждения, которые как бы необходимо использовать как основные положения. Например об обычных фонариках. Действительно, интерференционной картины (ИК) мы не увидим. Также не увидим, вопреки вашему утверждению, и при разделении света от одного фонарика, который вы уже назвали источником. Давайте рассматривать источники, при которых ИК можно наблюдать. Предлагаю в виде лазеров. Полагаю, вы рассматриваете их как источники когерентного излучения волн, т.е. в терминах волновой парадигмы света. В корпускулярной парадигме «когерентным»  можно назвать фотоны с одинаковыми (близкими) скоростями.
Далее вы предлагаете рассматривать фотоны как невзаимодействующие, неделимые, излученные атомами. А на каком основании? Это проверенные опытами утверждения или чьё-либо мнение, использованные как аксиомы? Я вам могу дать фото из «интерференционного» опыта, в котором световые пятна (картины) на экране изменяются на совсем небольшом расстоянии. Или пятно от луча лазера на расстоянии порядка сотни метров — в пятне явственно наблюдаются «интерференционные» линии. Они просто объясняется свойством взаимодействия частиц света. Они могут притягиваться, отталкиваться или не взаимодействовать друг другу. Последний случай относится к поляризованному свету. Свойство взаимодействия частиц света является причиной образования интерференционных картин. Аналогично и с электронами.
О делимости фотонов и их излучениях атомом. Когда будут опыты, показывающие на делимость/неделимость фотонов, тогда у нас будет основание обсуждать. Аналогично и с излучением атомами.
Полагаю, вы дадите свой, волновой, вариант образования ИК и возражения против представленного мной. И, конечно, ваше понимание что есть волны света.

[sergey_B_K]

О вопросах. В ваших вопросах содержаться утверждения, которые как бы необходимо использовать как основные положения. Например об обычных фонариках. Действительно, интерференционной картины (ИК) мы не увидим.  Также не увидим, вопреки вашему утверждению, и при разделении света от одного фонарика, который вы уже назвали источником.

Здесь сразу отмечу, что в опытах Майкельсона источником служила горелка, а не лазер. И получались прекрасные интерференционные полосы. И в учебниках описаны методы получения интерференционной картины между двумя параллельными зеркалами

http://nature.web.ru/db/msg.html?mid=1165186&uri=but7_21.html
При монохроматических лучах будут полосы одного цвета. При обычном свете каждая полоса расслаивается в спектр. Так что у меня всё нормально, а Вот Вам стоит подкорректировать посылку... 

В корпускулярной парадигме «когерентным»  можно назвать фотоны с одинаковыми (близкими) скоростями.

Это уже не базовая модель фотона и, тем более, не согласующаяся с релятивизмом. Давайте останемся на базовой концепции, чтобы Вы не бегали по кустам, спасая свои "изменения", уничтожающие и фотонную концепцию, и релятивизм. 

Далее вы предлагаете рассматривать фотоны как невзаимодействующие, неделимые, излученные атомами.

Это не я предлагаю, а фотонная концепция. По определению
"Фотон – фундаментальная частица, квант электромагнитного поля. В виде фотонов испускается и поглощается электромагнитное излучение. Фотон имеет свойства как частицы, так и волны. У него нет ни электрического заряда, ни массы. Фотон имеет определенную энергию Е = hν (h – постоянная Планка, равная 4.14·10-15 эВ·сек, ν – частота электромагнитных колебаний) и импульс, величина которого р = Е/с (с – скорость света, с которой всегда движется фотон в пустоте)".
Фотон
http://nuclphys.sinp.msu.ru/enc/e175.htm
 "с точки зрения квантовых представлений оптическое излучение можно рассматривать как фотонный кол­лектив, состоящий из фотонов в k-состояниях, т.е. как газ, состоящий из частиц с энергией  и импульсом k ".
1.3.2.  Корпускулярные свойства света. Фотоны
https://electrono.ru/1-3-2-korpuskulyarnye-svoystva-sveta-fotony-kvant_opt
Взаимодействие фотона с фотоном предполагается исключительно при посредстве вещества, т.е. фотон поглощается, другой фотон излучается.

А на каком основании? Это проверенные опытами утверждения или чьё-либо мнение, использованные как аксиомы?

Это мнение тех, абсурд которых Вы защищаете... В частности, это мнение и Ахиезера, изложенное им в базовой работе "Квантовая электродинамика" 
Там же указано, что фотон не может делиться. Только переизлучаться с изменением частоты, а значит, и энергии (у фотонщиков).
Так что всё не мной придумано...  Более того, моего здесь вообще нет.

Я вам могу дать фото из «интерференционного» опыта, в котором световые пятна (картины) на экране изменяются на совсем небольшом расстоянии. Или пятно от луча лазера на расстоянии порядка сотни метров — в пятне явственно наблюдаются «интерференционные» линии.

Хотел  бы видеть, но прежде саму схему, в которой это было получено... 
Остальные вопросы всплывут сами собой далее. Не стоит всё валить в одну кучу. Сначала утрясём базовую концепцию. 

[в.макаров]

При обычном свете каждая полоса расслаивается в спектр. Так что у меня всё нормально, а Вот Вам стоит подкорректировать посылку...  Это уже не базовая модель фотона и, тем более, не согласующаяся с релятивизмом. Давайте останемся на базовой концепции, чтобы Вы не бегали по кустам, спасая свои "изменения", уничтожающие и фотонную концепцию, и релятивизм.).
Так что всё не мной придумано...  Более того, моего здесь вообще нет.:)Хотел  бы видеть, но прежде саму схему, в которой это было получено...  :)Остальные вопросы всплывут сами собой далее. Не стоит всё валить в одну кучу. Сначала утрясём базовую концепцию. 

Извините, что оставил без внимания ваши лирические отступления.
О базовой концепции. Вы упорно предлагаете взять в основу рассмотрения корпускулярного света некую базовую концепцию. Со ссылками на учебную литературу. Если вам интересна принятая в современной науке концепция света , то она изложена Р. Фейнманом в известных вам его лекциях. Конкретно, в лекции № 6. Его суждения об электронах и частицах света при обсуждении их свойств в опытах со щелями совпадают. "Свет также ведёт себя как поток частиц ..." Заметил, что волновые свойства света и электронов относятся к волновым уравнениям, применяемых в описании волн воды, т. е. к волновым уравнениям. Потому вы можете оспаривать принятую концепцию свет-частицы. Концепцию свет-волны вам нужно защитить.
В парадигме свет-частицы «притягивание» волновых свойств, по моему мнению, из-за невозможности дать адекватное объяснение причины «интерференционных» картин. По простой причине: игнорируется свойство взаимодействия частиц. Это свойство света явно наблюдается в указанных мной опытах, мной же и проведенных. Фото представлю. При таком свойстве объяснение «интерференционных» картин оказывается, как по Фейнману, «простым до глупости».
Смею заметить, вы так и не дали свои представления о волнах света. И исходные положения для понимания, что есть волны света. Волны чего? Волны в чём?