Попробуем зайти с другой стороны.
Двже Ваша
исходная формулировка задачи о вращающемся стержне как и
последующая - весьма корявые, но я не стал придираться, выделив главное.
ВЫ же, не разобравшись в этом главном, продолжаете корявить формулировки "заходя с другой стороны" - и с этой стороны у Вас тоже получается долбостебство.
Мы видим кривой стержень в наблюдающей ИСО в момент t0=0.
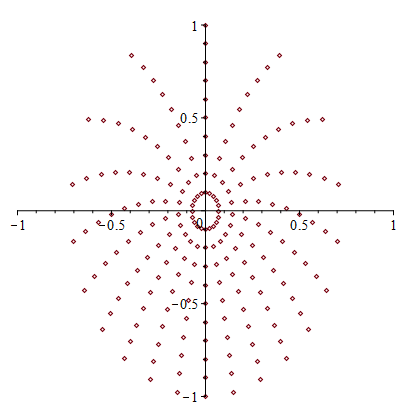
Координаты кривого стержня (c t0,ri), где i=1..10.
ВО первых, мы видим выставленный Вами график, на котором изображены положения (координаты) 10 точек стержня, через каждые 1/20 периода (20 полуветвей, объединяющихся попарно, две из которых вполне прямые - для положения стержня перпендикулярно движению, + центральная точка вращения, в которой на графике условно совмещаются все положения, разноместные в системе где стержень и вращается и перемещается).
Какую пару полуветвей ВЫ ставите в соответствие моменту t0=0 ?
Во-вторых, по поводу термина "видим" я уже писал
И даже правильно заметили, что аналогия не вполне корректная, потому что "разглядывание" или "фотографирование" обязательно подразумевает фактор запаздывания сигнала с места событий до места наблюдения, а в исходной постановке задачи события регистрируются там где происходят - в пространственно-временной сетке координат выбранной ИСО.
Мне показалось, что Вы хотя бы в этом разобрались - но там по-видимому был Ваш дублер, а здесь Вы лично продолжаете долбостебить на тему "мы видим..."
В ИСО, где этот стержень находится, он прямой.
Уже выяснили раньше, что стержень однозначно прямой (в любой произвольный момент времени) в системе, где он только вращается, без перемещения.
Но разве стержень НЕ находится и в системе наблюдения (выбираемой произвольно), где он и вращается и перемещается ?
ВЫ опять альтернативно намекаете, что ИСО где стержень только вращается - это выделенная система, в которой стержень "реально находится" и "реально прямой" - но это НЕ СТО, в которой ВСЕ ИСО РАВНОПРАВНЫ.
Делаем обратное ПЛ преобразование этих координат.
Какая форма стержня должна получится после преобразования?
И опять Вы смешали в один клубок недоразумений
вопрос о формальных преобразованиях 4-х координат точек стержня получающихся в результате ПЛ из исходных ОДНОВРЕМЕННЫХ координат (с сохранением 4-х интервала, но с нарушением одновременности)
и
вопрос о форме стержня, которая в другой ИСО должна определяться по пространственным координатам, взятым в этой ИСО одновременно.
На оба этих вопроса я уже отвечал Вам раньше:
В каждой ИСО форма тела задается координатами тела в ОДИН момент времени - это и есть РЕАЛЬНАЯ ФОРМА тела в ЭТОЙ ИСО.
Поэтому лампочки, зажигаемые на стержне одновременно в ИСО1 где стержень только вращается, дают прямую форму стержня в ЭТОЙ ИСО1 (по Вашему п.1).
Но в соответствии с СТО в другой ИСО2 эти же лампочки вспыхивают НЕ ОДНОВРЕМЕННО (по Вашему п.2) поэтому НЕ определяют ФОРМУ стержня - хотя численные значения координат вспышек укладываются на одной пространственной прямой.
С другой стороны, лампочки зажигающиеся одновременно в ИСО2 где вращающийся стержень перемещается (по Вашему п.1) и дающие там реально кривую форму стержня в одной его фазе, в ИСО1 где стержень только вращается, по СТО зажигаются НЕ одновременно (по Вашему п.2), поэтому тоже не могут служить для определения формы стержня в ИСО1 (там стержень реально прямой).
Обо всем этом уже писалось раньше, но ВЫ снова все СОЗНАТЕЛЬНО запутали "зайдя с другой стороны" - как 100% долбостеб - вынуждая оппонента (меня) снова распутывать клубок ВАШИХ недоразумений.
ПОдозреваю, что и далее ВЫ намерены вести "обсуждение" в такой же образцово-показательной долбостебской манере - мне это не нужно.
Я здесь участвовал с позиций СТО только потому, что ВЫ ПЕРЕВИРАЛИ СТО, а корифеи и знатоки СТО не захотели сами с Вами возиться.
Со мной дискуссию можете продолжить если Вы признаете что не правы в ВАШЕМ толковании ФОРМЫ тела по СТО (в указанном выше понимании).


