Звездолёт летит относительно ИСО со скоростью \(v_p=0.8\) света.
На звездолёте вращается относительно центра масс стержень. Скорость конца стержня \(v_e=0.9\).
Радиус конца стержня \(r_0=1\) м. Вектор скорости звездолёта лежит в плоскости движения стержня и его угол равен
\(\beta = 0^\circ\) относительно оси \(x\) в ИСО звездолёта. Оси систем отсчёта сонаправлены.
Вычислить энергию стержня в подвижной и неподвижной ИСО. Стержень механически абсолютно жесткий.
Обязательное условие, при решении задачи применить уравнение формы стержня в ИСО наблюдения.
Координаты стержня в ИСО звездолёта. Центр масс стержня покоится. Система отсчёта в центре масс.
\(x_1=r~cos(\omega~t_1+\phi)\);
\(y_1=r~sin(\omega~t_1+\phi)\).
Скорость стержня в ИСО звездолёта.
\(v_{1x}=-\omega~r~sin(\omega~t_1+\phi)\);
\(v_{1y}=\omega~r~cos(\omega~t_1+\phi)\).
Энергия стержня в ИСО звездолёта.
\(\displaystyle E_1=\int\limits_0^{r_0} \frac{\sigma~c^2}{\sqrt{1-\frac{v_{1x}^2+v_{1y}^2}{c^2}}}~dr=\int \limits_{0}^{r_0} \frac{\sigma~c^2}{\sqrt{1-\omega^2~r^2 / c^2}}~dr=\frac{2\sigma~c^3}{\omega} atan \left(\frac{c}{\omega~r_0} \left(1-\sqrt{1-\omega^2~r_0^2/c^2} \right) \right)=\frac{\sigma~c^3}{\omega} asin \left(\frac{\omega~r_0}{c}\right) \approx \sigma~r_0~c^2+\frac{\sigma~r_0~(\omega~r_0)^2}{6}\) (На малых оборотах).
Для любого положения стержня энергия будет равна
\(E_1(0)+E_1(\pi)=2E_1(0)=223.953903\).
Рассмотрим стержень с точки зрения покоящегося наблюдателя.
В окне звездолёта он видит сокращенный стержень по оси x и номинальной длины по оси y.
Система отсчёта в центре масс.
\(\displaystyle x_k=\frac{r}{\gamma}~cos(\omega~t_1+\phi)\);
\(y_k=r~sin(\omega~t_1+\phi)\).
Эти уравнения определяют форму
прямого стержня в момент
\(t_1\).
Дифференцируем, вычисляем кинематические скорости в окне звездолёта.
\(\displaystyle v_{xk}=\frac{dx_k (t_1)}{dt}=\frac{dx_1(t_1)}{\gamma~dt}=\frac{v_{1x}~dt_1}{\gamma~dt}=\frac{v_{1x}~dt_1}{\gamma^2}\left(dt_1+\frac{V~dx_1}{c^2}\right)^{-1}=\frac{v_{1x}}{\gamma^2}\left(1+\frac{V~v_{1x}}{c^2}\right)^{-1}\);
\(\displaystyle v_{yk}=\frac{dy_k (t_1)}{dt}=\frac{dy_1(t_1)}{dt}=\frac{v_{1y}~dt_1}{dt}=\frac{v_{1y}~dt_1}{\gamma}\left(dt_1+\frac{V~dx_1}{c^2} \right)^{-1}=\frac{v_{1y}}{\gamma}\left(1+\frac{V~v_{1x}}{c^2} \right)^{-1}\).
Вычисляем энергию в неподвижной ИСО.
\(\displaystyle E=\int \limits_0^{r_0} \frac{\sigma~c^2}{\sqrt{1-\frac{(v_{xk}+V)^2+v_{yk}^2}{c^2}}}~dr\).
Для любого положения стержня энергия будет равна
\(E(0)+E(\pi)=373.256505\).
\(\displaystyle (E(0)+E(\pi)) \frac{1}{\gamma}=E_1(0)+E_1(\pi)=223.953903\). Между энергиями правильное соотношение. Это инвариант.
Обратите внимание, что
\(\displaystyle v_{x}=v_{xk}+V=\frac{v_{1x}}{\gamma^2}\left(1+\frac{V~v_{1x}}{c^2}\right)^{-1}+V=\left(\frac{v_{1x}}{\gamma^2}+V\left(1+\frac{V~v_{1x}}{c^2}\right) \right) \left(1+\frac{V~v_{1x}}{c^2}\right)^{-1}=\left(v_{1x} \left(1-\frac{V^2}{c^2}\right)+V\left(1+\frac{V~v_{1x}}{c^2}\right)\right) \left(1+\frac{V~v_{1x}}{c^2}\right)^{-1}=\)\(\displaystyle =\left(v_{1x}-\frac{V^2}{c^2}v_{1x}+V+\frac{V^2~v_{1x}}{c^2}\right) \left(1+\frac{V~v_{1x}}{c^2}\right)^{-1}=\left(v_{1x}+V\right)\left(1+\frac{V~v_{1x}}{c^2}\right)^{-1}\).
\(\displaystyle v_{y}=v_{yk}=\frac{v_{1y}}{\gamma}\left(1+\frac{V~v_{1x}}{c^2}\right)^{-1}\). Получили правило сложение скорости.
http://bolshoyforum.com/forum/index.php?topic=606376.msg9643382#msg9643382http://bolshoyforum.com/forum/index.php?topic=608330.msg9192692#msg9192692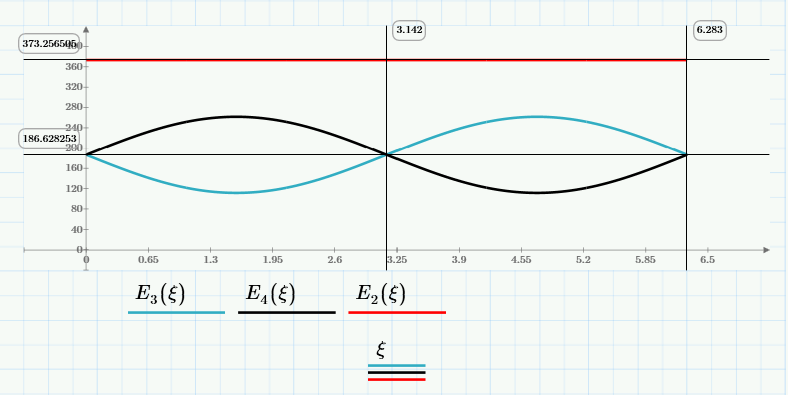
\(E_3\) и
\(E_4\) энергия половин стержня за оборот в покоящейся ИСО.
\(E_2=E_3+E_4\) суммарная энергия относительно центра масс, постоянная и не может быть переменной в этой задаче.
Инвариантность 4-импульса проверена.
Интервал равен
\(s^2=c^2~t_1^2-r^2=inv\).
Модуль импульса одной половины стержня в системе отсчёта звездолёта
\(\displaystyle p=\int\limits_{0}^{r_0} \frac{\sigma~\omega~r}{\sqrt{1-\omega^2~r^2 / c^2}}~dr=\frac{\sigma~\omega~r_0^2}{\sqrt{1-\omega^2~r_0^2 / c^2}-1}+\frac{2\sigma~c^2}{\omega}=\frac{\sigma~c^2}{\omega} \left(1-\sqrt{1-\omega^2~r^2 / c^2}\right)\).
\(\displaystyle \int \limits_{-r_0}^{r_0} \frac{\sigma~\omega~r}{\sqrt{1-\omega^2~r^2 / c^2}}~dr=0\).
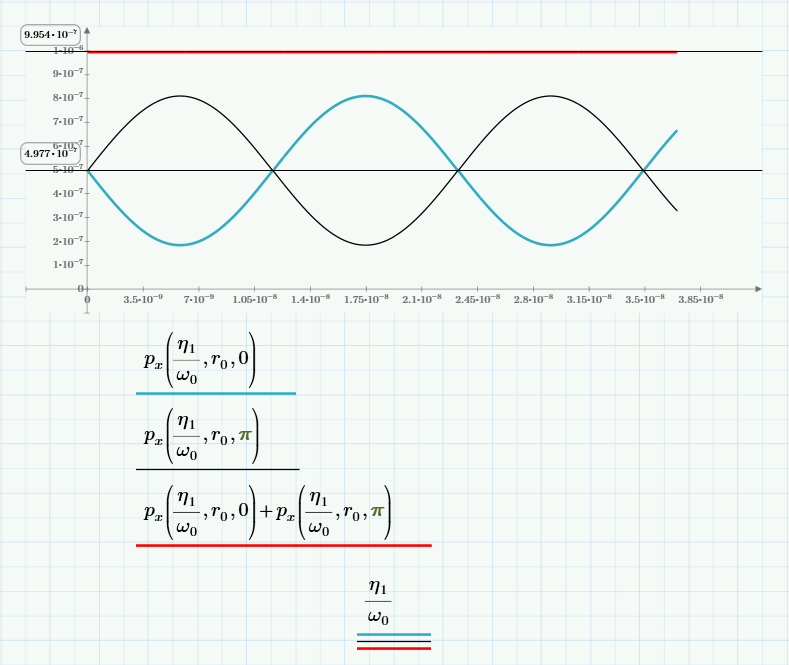
Импульсы постоянны относительно центра масс.
