Может достаточно уже махать кулаками и подумать, когда и кто начал этот "кулачный бой"?
А начал его тот самый, не, не Мюнхгаузен, а Галилей.
Продолжим чтение
Рассмотрим две системы отсчёта: K и K{}. Координатные оси этих систем сонаправлены. Систему K будем считать неподвижной. Система K{} движется относительно неё с постоянной скоростью \vec{v} вдоль общего направления осей X и X{} (рис. 1)

В тот момент, когда начала координат O и O{} совпадали, часы обеих систем были выставлены на ноль и запущены. Стало быть, часы в системах K и K{} идут синхронно, показывая одно и то же время t. В момент времени t расстояние OO{} равно vt.[/b]
Но, позвольте, а что такое
vt?
Нет! Ну, конечно, я понимаю, что это взято из формулы скорости, но в таком виде ОНО НЕ ПРИМЕНИМО.
Рассмотрим простенькую, но поучительную иллюстрацию
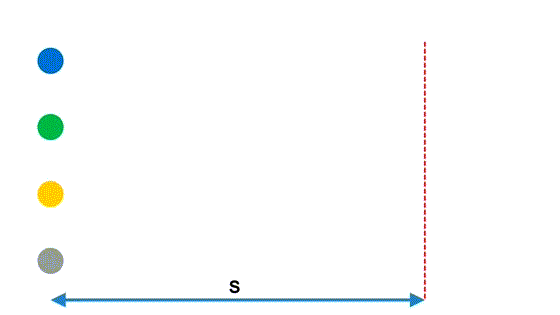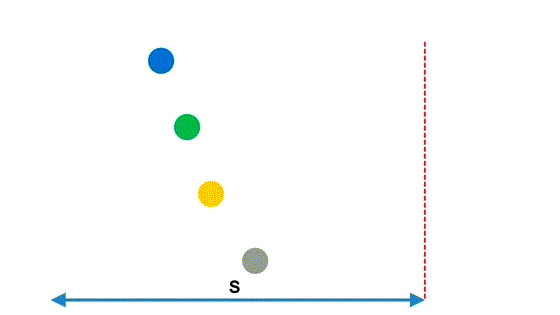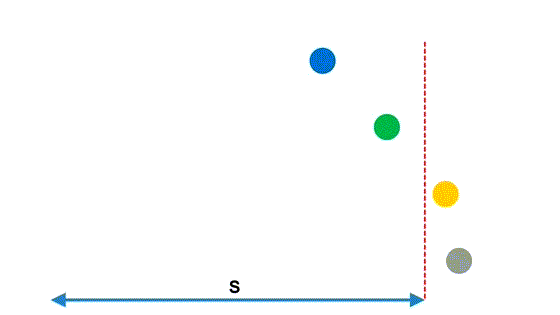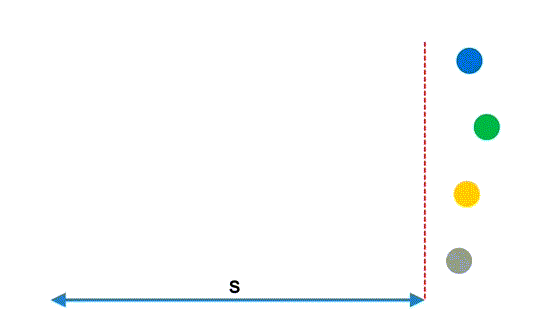
Расстояние у всех шаров одинаковое, но какой-то шар оказывается быстрее других.
Предположим, что самый нижний шар потратил 12[ ] - тут размерность не важна. Это могут быть годы, секунды и т.д.
Тогда для этого шара скорость будет равна 100 - дистанция и тоже не важно в каких единицах, деленая на 12, т.е 100\12 - для нижнего шара.
Для второго - 100\13,
для третьего 100\14, и последнего 100\15
Мы получили несколько дробей -
100\12, 100\13, 100\14, 100\15, Из Закона математики мы знаем, чтобы сравнить дроби нужно привести их к одному знаменателю.Но мы числительное каждой дроби разделим на её знаменатель. Знаменатели будут равны ЕДИНИЦЕ.1-й 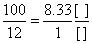 2-й
2-й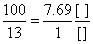
3-й 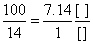
и так далее
Но единицу в знаменателе не пишут, оставляя только числитель.
О том, что в знаменателе единица, напоминает дробная размеренность.
А что же делает Галилий?
Вместо расстояния - "S" он заменяет его произведением 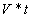
Но имел ли он право так делать?