Обсуждение:Кризис теоретической физики: признаки, причины, виновники (частный взгляд со стороны на академическую и вузовскую науку)
Очередное кликушество о "кризисе теоретической физики" выдвигаемое человеком, не имеющем ни малейшего представления даже о теоретическое механике, не заслуживало бы внимания даже в форме опровержения, если бы не следующее удручающее обстоятельство. Ни в одной из бесчисленных статей Петрова в Научном журнале их автор не продемонстрировал способности не только к правильному решению задач механики, но даже к их постановке. Между тем при минимальной аккуратности в постановке задачи Автор имел бы шанс избежать детских ошибок, последовательно приводящих к тому, что ни одно из его решений не имеет ни физического, ни математического смысла.
Содержание
Постановка задачи
Рассмотрим постановку задачи, в крайне противоречивой форме описанной в главе "Гравитационный двигатель с неизменным потенциалом рабочей массы". Маховик в виде плоского круглого диска массы M и радиусом R, закрепленный на горизонтальной оси, раскручивается до некоторой "резонансной" частоты и затем переводится в свободное вращение. На диске на двух взаимно перпендикулярных направляющих, проходящих через центр диска, могут двигаться два тела, каждое массой m, закрепленных на пружинах жесткости k. По смыслу задачи, после раскрутки маховика до резонансной частоты, тела начинают движение из центра диска и начинается "резонансная" раскачка колебаний за счет действия силы тяжести, ускорение которой равно g.
Обозначая координату первого из тел вдоль его направляющей с выбором нуля в центре как x, аналогично для второго тела вводим координату y и, наконец, обозначаем буквой 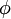 угол между осью, по которой движется тело x, с горизонтальным направлением. В начальный момент времени считаем заданными нулевые значения для x, y и начальное "резонансное значение" для частоты вращения:
угол между осью, по которой движется тело x, с горизонтальным направлением. В начальный момент времени считаем заданными нулевые значения для x, y и начальное "резонансное значение" для частоты вращения:
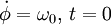
Точка здесь и далее обозначает дифференцирование по времени. Задача полностью поставлена. Лагранжиан системы, очевидно, имеет вид:
![L=\frac{\dot{\phi}^2}2\left[\frac{MR^2}2+m(x^2+y^2)\right]+\frac{m}2(\dot{x}^2+\dot{y}^2) -\frac{k}2(x^2+y^2)-mg\left[x\sin(\phi)+y\cos(\phi)\right]](/wiki/images/math/4/7/c/47c54fd61c89c0fa1dbb360d3d756e91.png)
Уравнения движения
Уравнения движения получаем методом Лагранжа. Помимо уравнений для x, y дадим также выражение для их комплексной линейной комбинации, z=x+iy:
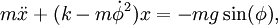
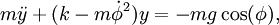
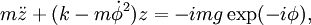
(1)
вместо же уравнения для 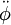 , определяюшего систематическое замедление вращения по мере раскачки колебаний
, определяюшего систематическое замедление вращения по мере раскачки колебаний
![\frac{d}{dt}\left\{\dot{\phi}\left[\frac{MR^2}2+m(x^2+y^2)\right]\right\}=-mg\left[x\cos(\phi)-y\sin(\phi)\right]=-mg\Re[z\exp(i\phi)],](/wiki/images/math/a/c/6/ac6c61c86be16a0cf5600034a0ac3a58.png)
(2)
можно воспользоваться сохранением энергии для системы с Лагранжианом, не зависящим явно от времени:
![\frac{\dot{\phi}^2}2\left[\frac{MR^2}2+m(x^2+y^2)\right]=\frac{\omega_0^2}2\frac{MR^2}2-\frac{m}2(\dot{x}^2+\dot{y}^2) -\frac{k}2(x^2+y^2)-mg\left[x\sin(\phi)+y\cos(\phi)\right]](/wiki/images/math/4/0/2/40286664cd7966027549d93de34b05f8.png)
Или, через комплексное z (звездочка обозначает комплексное сопряжение, введено также обычное обозначение для действительной части комплексного числа):
![\dot{\phi}^2=
\frac{\omega_0^2\frac{MR^2}2-{m}\dot{z}\dot{z}^* -{k}zz^*-mg\Re\left[-iz\exp(i\phi)\right]}
{\frac{MR^2}2+mzz^*}](/wiki/images/math/0/3/7/0375b99270dda43654ec34c80b2ef4c1.png)
(3)
Решения в отсуствие диссипации
Нетрудно найти решение полученных уравнений в виде вращения с постоянной частотой 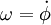 . Имеем:
из (1):
. Имеем:
из (1):
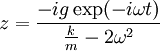
Правая часть (2) при этом обращается в ноль, что согласуется с предположением о постоянстве частоты. На первый взгляд может показаться что выбор "резонансной частоты" 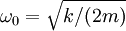 в качестве начальной частоты вращения (поразительно, но в критикуемой работе выражение для резонансной частоты вообще не получено) допускает неограниченную (точнее ограниченную долько диссипативными процессами) раскачку колебаний. Однако это грубейшая ошибка, возникшая из-за забвения о законе сохранения энергии или, что то же самое, о соотношении (3) для частоты вращения. В действительности при таком выборе для начальной частоты вращения после некоторого роста колебания частота вращения в соответствии с (3) существенно понизится, после чего система выйдет из резонанса и рост колебаний прекратится (это хорошо известный и описанный в учебниках эффект нелинейного самоограничения резонанса). Нетрудно показать, что при любом выборе начальной частоты вращения, установившаяся после роста колебаний частота вращения будет либо несколько ниже, либо несколько выше резонансной, но никогда не попадет точно в резонанс.
в качестве начальной частоты вращения (поразительно, но в критикуемой работе выражение для резонансной частоты вообще не получено) допускает неограниченную (точнее ограниченную долько диссипативными процессами) раскачку колебаний. Однако это грубейшая ошибка, возникшая из-за забвения о законе сохранения энергии или, что то же самое, о соотношении (3) для частоты вращения. В действительности при таком выборе для начальной частоты вращения после некоторого роста колебания частота вращения в соответствии с (3) существенно понизится, после чего система выйдет из резонанса и рост колебаний прекратится (это хорошо известный и описанный в учебниках эффект нелинейного самоограничения резонанса). Нетрудно показать, что при любом выборе начальной частоты вращения, установившаяся после роста колебаний частота вращения будет либо несколько ниже, либо несколько выше резонансной, но никогда не попадет точно в резонанс.
Решения при наличии диссипации
Эта часть работы Петрова совершенно абсурдна и возникла как следствие грубого игнорирования уравнения движения (2). При добавлении в уравнение (1) пропорциональной скорости силы трения 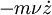 это уравнение принимает вид:
это уравнение принимает вид:
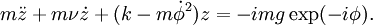
(4)
Сразу отмечу что работа, совершаемая силами трения за единицу времени, отрицательна и равна
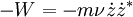
Уже хотя бы из этих соображений представляется очевидным, что поддержание постоянной (особенно резонансной) частоты вращения в системе с потярями невозможно без постоянно затрачиваемой внешней мощности. Действительно, решение уравнения (4) для постоянной частоты вращения получить нетрудно:
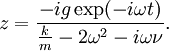
Однако правая часть (2) при этом не отнюдь не обращается в ноль! Для поддержания частоты вращения постоянной в правую часть (2) необходимо добавить развиваемый некоторым внешним двигателем постоянно действующий момент сил, равный, очевидно, ![T=mg\Re[z\exp(i\phi)]](/wiki/images/math/b/f/7/bf7072a20a19b852b6914b603379e3a7.png) . Вычисление действительной части дает:
. Вычисление действительной части дает:
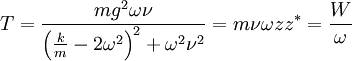
Мощность, которую должен развивать внешний двигатель для поддержания такого момента сил равна 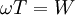 ! Таким образом мощность диссипации энергии колебаний (что и является полезной мощностью данного "гравитационного двигателя") всецело заимствуется из внешнего двигателя - а если последний отсутствует, поддержание стационарной резонансной частоты вращения и раскачка колебаний до диссипативного предела не представляются возможными.
! Таким образом мощность диссипации энергии колебаний (что и является полезной мощностью данного "гравитационного двигателя") всецело заимствуется из внешнего двигателя - а если последний отсутствует, поддержание стационарной резонансной частоты вращения и раскачка колебаний до диссипативного предела не представляются возможными.
О невозможности извлечения энергии из гравитационного поля
Домножим первое из уравнений (1) на 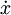 . Правая часть уравнения - это работа совершаемая за единицу времени силой тяжести над частицой x. Аналогично, домножим второе из уравнений (1) на
. Правая часть уравнения - это работа совершаемая за единицу времени силой тяжести над частицой x. Аналогично, домножим второе из уравнений (1) на 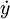 . Правая часть уравнения - это работа, совершаемая за единицу времени силой тяжести над частицой y. Наконец, домножим уравнение (2) на
. Правая часть уравнения - это работа, совершаемая за единицу времени силой тяжести над частицой y. Наконец, домножим уравнение (2) на 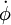 . Среднее из выражений это будет работа, совершаемая моментом силы тяжести над вращаюшейся системой. Суммируя эти три члена получаем полную работу, совершаемую гравитиционной силой за ежиницу времени, которую преобразуем следующим образом:
. Среднее из выражений это будет работа, совершаемая моментом силы тяжести над вращаюшейся системой. Суммируя эти три члена получаем полную работу, совершаемую гравитиционной силой за ежиницу времени, которую преобразуем следующим образом:
![-\dot{x}mg\sin(\phi)-\dot{y}mg\cos(\phi)-\dot{\phi}mg\left[x\cos(\phi)-y\sin(\phi)\right]=-\frac{dU}{dt},\quad U=mg\left[x\sin(\phi)+y\cos(\phi)\right],](/wiki/images/math/3/d/c/3dc6e15447691e06c2b36b93d5f6a6c9.png)
где введена потенциальная энергия масс x, y в гравитационном поле, 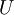 . Интегрируя по времени, приходим к потверждению общеизвестного факта: работа совершаемая силой тяжести за любой интервал времени равна взятому с обратным знаком изменению потенциальной энергии системы в поле силы тяжести и никакая энергия сверх этой из гравитацонного поля извлечена быть не может. В данном случае во всех решениях потенциальная энергия в поле силы тяжести не зависит от времени, поэтому суммарная работа совершаемая силой тяжести, равна нулю: правильно вычисленная положительная работа по раскачке колебаний компенсируется упущенной в статье Петрова работой по торможению вращения.
. Интегрируя по времени, приходим к потверждению общеизвестного факта: работа совершаемая силой тяжести за любой интервал времени равна взятому с обратным знаком изменению потенциальной энергии системы в поле силы тяжести и никакая энергия сверх этой из гравитацонного поля извлечена быть не может. В данном случае во всех решениях потенциальная энергия в поле силы тяжести не зависит от времени, поэтому суммарная работа совершаемая силой тяжести, равна нулю: правильно вычисленная положительная работа по раскачке колебаний компенсируется упущенной в статье Петрова работой по торможению вращения.
Заключение
Не боясь прослыть ретроградом, заявлю: не бывает гравитационных двигателей! Бывают самоуверенные и безграмотные люди, которые не умеют решать и даже правильно выводить уравнения движения для простейших механических задач.
Постскриптум
Автор в "Ответе" напрасно посчитал, что задачу механики можно решать не посредством вывода и решения уравнений а путём словесных манипуляций.
Конкретно, чтобы "оценить затраты энергии на поддержание стабильной частоты вращения", неообходимо, во-первых, вывести динамическое уравнение, которому подчиняется частота вращения. Это выведенное мною уравнение (2) для углового момента количества движения. Читатель вправе рассчитывать, что автор научной публикации о вращательном движении знаком с понятием углового момента количества движения и умеет составлять и решать динамическое уравнение, которое определяет изменение во времени углового момента количества движения (левая часть уравнения 2) через приложенный к системе момент внешних сил (см правую часть уравнения 2).
В данном случае момент силы тяжести, T, приложенный к системе (а отнюдь не обсуждаемая Автором бессмысленная комбинация "тангенциальных скоростей и ускорений"), не равен нулю и постоянно совершает работу по торможению вращения, с мощностью, равной W (см мой раздел Решение при наличии диссипации). Единственный способ противодействия - это приложить с помощью внешнего двиателя момент силы, -T, на что необходимо постоянно затрачивать мощность, равную 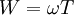 .
.
Остается добавить, что в обозначениях автора (использование 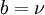 ) и в условиях резонанса (знаменатель в выражении для T в этом случае равен
) и в условиях резонанса (знаменатель в выражении для T в этом случае равен 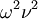 ) выражение для мощности внешнего двигателя равно
) выражение для мощности внешнего двигателя равно 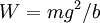 , что в четыре раза превышает мощность
, что в четыре раза превышает мощность 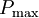 , которую Автор рассчитывает извлечь из своего двигателя в качестве полезной.
, которую Автор рассчитывает извлечь из своего двигателя в качестве полезной.
Напоминаю также, что общеоскорбительного характера замечания Автора по поводу метода Лагранжа и закона сохранения энергии не заменяют (и тем более не отменяют) необходимости составления и решения уравнений движения (в том числе, если необходимо, уравнения моментов) как единственно легитимного способа анализа механических систем. К сожалению, Автор последовательно пренебрегает этим принципом, что делает любые его работы заведомо смехотворными.
Ответ автора статьи
Оппонент,применяя лагранжев формализм, постулирует соблюдение закона сохранения энергии и в результате несложных манипуляций получает «совершенно неожиданный» вывод: следовательно, энергия в систему не поступает! Оппоненту даже заранее «Лагранжиан известен», хотя мне, как конструктору системы, синтезирующему её так, чтобы получить требуемые свойства, нет. Скажу больше: мне об этой функции ничего не захочется узнать и после решения задачи, поскольку она к этой задаче никакого отношения не имеет. В задаче о брахистохроне я этой функцией воспользовался бы. В других вариационных задачах взял бы функцию, аналогичную функции Лагранжа, но уже не в виде разности, а в виде суммы кинетической и потенциальной энергии. Но сейчас я в услугах этого аппарата не нуждаюсь, ибо он сюда элементарно не подходит. А нужно мне (считайте, что «дано»), чтобы решением задачи (в неподвижной системе координат) были функции вида:
x = cos(wt) exp(iwt); dx/dt = –w sin(wt) exp(iwt) + iw cos(wt) exp(iwt); d²x/dt² = –2w² cos(wt) exp(iwt) – i2w² sin(wt) exp(iwt); y = –i sin(wt) exp(iwt); dy/dt = – i w cos(wt) exp(iwt) + w sin(wt) exp(iwt); d²y/dt² = i 2w² sin(wt) exp(iwt) + 2w² cos(wt) exp(iwt).
Поэтому во вращающейся системе координат я реализую резонансный процесс, подчиняющийся следующим уравнениям (пока беру только радиальные изменения одномерных координат в качестве основного эффекта работы системы; о побочных эффектах – потом):
d²α/dt²+b dα/dt+w²α= –g sin(wt), d²β/dt²+b dβ/dt+w²β= –ig cos(wt), где b – удвоенный коэффициент затухания свободных колебаний в системе, [–gsin(wt)–igcos(wt)]=–igexp(–iwt) – ускорение свободного падения на поверхности Земли (во вращающейся системе координат, с фазовым множителем обратного вращения, разложенным по осям координат).
Естественно, при наличии диссипативных потерь и полезной нагрузки резонансная частота, отвечающая уравнениям движения, отличается от частоты свободных колебаний в системе без потерь. Решениями указанных выше уравнений являются функции:
α=(g/bw)cos(wt), β= –i(g/bw)sin(wt).
Как видим, мы получили то, что хотели. Взяв двойной запас, получаем следующий теоретический предел полезной (активной) мощности гравитационно-резонансного двигателя данного типа для работы в наземных условиях при величине суммарной рабочей массы m: Р max = mg²/4b.
А теперь проверим, не «съедят» ли побочные эффекты всю поступающую в систему энергию. В невращающейся системе координат нам не придётся иметь дело с кориолисовыми ускорениями. К тому же, мы уже заранее продифференцировали координаты двух половинок рабочих масс, так что теперь надо только вычислить скалярные произведения тангенциальных составляющих скоростей и ускорений, чтобы оценить затраты энергии на поддержание стабильной частоты вращения. Для отдельной массы m имеем:
П=(2mgw/b) sin(wt) • (g/b) cos(wt) = (mg²w/b²) sin(2wt).
Как видим, среднее значение мощности, развиваемой силами торможения-ускорения, за полпериода основного вращения системы равняется нулю. При наличии более, чем двух частей рабочей массы, а также другими мерами можно добиться достаточно стабильной частоты вращения, а значит, и устойчивой работы системы с полезным выходом энергии. Естественно, предлагаемое техническое решение не единственно возможное.
От Автора:
Более подробный ответ на вышеприведённую критику содержится в статьях ЭБФ -
"БЕЗОПОРНОЕ ДВИЖЕНИЕ И ГРАВИТАЦИОННАЯ ЭНЕРГЕТИКА: ТЕОРИЯ И ЭКСПЕРИМЕНТЫ, ПОДТВЕРЖДАЮЩИЕ ИХ РЕАЛЬНОСТЬ" и "БРАХИСТОХРОНА: НАЧАЛО И КОНЕЦ ЛАГРАНЖЕВО-ГАМИЛЬТОНОВОЙ МЕХАНИКИ".