Новые сообщения

Культура

• Goblin: Утомлённые сексом на костях отцов и дедов 2
• Политические анекдоты
• Сергей Капица: «Россию превращают в страну дураков»
• Яркие кинопремьеры и запрещённые советские фильмы
• В. Работнова: Воспитание идеального электората
• Rubliovka War
• РПЦ цензурирует Пушкина
• В. Бортко: Я хочу снять кино про Сталина
• В. Голышев: Пребиотики
• М. Полторанин: Власть в тротиловом эквиваленте. Наследие царя Бориса
• К. Эрнст: Одиночество...
• Гражданин поэт
• Как Губенко ставит Чиполлино на колени
• РАН о буржуазной идеологии РФ
• Украинство - форма безумия
• Словарик для выпускников ВГИКа
• А.Кунгуров: автор фильма БабальонЪ Месхиев воровал у ветеранов
• А. Кунгуров: «Битва за Севастополь» - гламурное дерьмо для идиотов
• Сексот ФБР Элвис Пресли
• Кобзарь, царь, Белинский и г'усские националисты
• Карамазовы дворяне, не вписавшиеся в рынок
• Черная метка российской оппозиции
• Проф. Преображенский - все еще ваш герой?
• Несвоевременные мысли товарища Горького. Часть 1
• Несвоевременные мысли товарища Горького. Часть 2
• Несвоевременные мысли товарища Горького. Часть 3
• А. Кунгуров: Четыре танкиста и приблудная баба
• Солженицын проклят своим народом
• Как в России введут аутодафе
• 12-серийный фильм «Зорге»
• Тля советской интеллигенции
• Вставайте, люди русские!
• Эпитафия Даниилу Гранину
• В РФ сняли худфильм про Путина
• Калашников: человек, автомат и говно-фильм
• Большая перемога на культурно-идеологическом фронте
• Закономерный финал любого царя
• Туристы на Солнцепёке
• Классово близкие авторы
• Чем хуже – тем лучше. Господь, жги!
• Z-гитлеровская поэзия Путина

Религия и Философия

• В. Иванов: Христианская церковь – страшная угроза свободе слова.
• В. Иванов: О монашестве
• Путин и "безбожники" Свердловска
• В. Иванов: Заявление в прокуратуру о признании ветхого завета экстремистской литературой
• В. Иванов: Реплика
• В. Иванов: Сопроводиловка
• В. Иванов: Состояние
• В. Иванов: Оценка акции
• Житель Ставрополя потребовал объявить Ветхий Завет экстремистской литературой
• Кирилл Решетников: Ветхий запрет
• В. Иванов: Ответ Ковельману
• Как жировала Русская православная церковь.
• В. Иванов: Наша задача - протащить Ветхий завет Библии на суд.
• Жалоба на бездействие Тимирязевского межрайонного прокурора г. Москвы
• В. Иванов: Мои комментарии на блогах Соловьёва и др
• Майк Филлон: Физиономия Христа
• Экстремисты в патриархии?
• Дворец патриарха в вырубленном заповеднике
• Благодатный огонь современного Иерусалима является рукотворным
• Е. Ф. Грекулов: Православная инквизиция в России
• Е. Шацкий: РПЦ и сожжения
• Е. Шацкий: Церковь, наука и просвещение в России XIX в.
• Архиепископ С. Журавлев: Не могу молчать – РПЦ и гомосексуализм!
• НТВ запретил показывать программу с Невзоровым о церкви
• Корпорация «церковь»
• Его Святейшество Патриарх Табачный и Аалкогольный Кирилл
• Осторожно: богохульство! Открытая студия, 5 канал
• Одеваемся скромнее? Открытая студия, 5 канал
• С. Соловьёв, Д. Субботин: Извращение к истокам
• Е. Ф. Грекулов: Нравы русского духовенства
• Е. Ф. Грекулов: Православная церковь — враг просвещения
• А. Солдатов: За что рабу Божьему Кириллу благодарить «раба на галерах»
• С. Бычков: История православного возрождение России
• Патриарх Кирилл оказался рейдером
• nevzorov.tv: Уроки атеизма
• РПЦ верный друг всех оккупантов России
• РПЦ как субъект экономической деятельности
• Pussy Riot первый инквизиторский процесс на постсоветском пространстве
• Поп из ХХС совратил прихожанку
• ОЗПП просит проверить деятельность Фонда ХХС
• Власти Карелии сажают в психушки и тюрьмы атеистов
• Безнаказанность РПЦ
• Нравственные ценности РПЦ
• Открытое письмо патриарху Кириллу
• Православные священники избивают бабушек
• Ю. Латынина: Невеликие инквизиторы
• К Дешнер: Криминальная история христианства
• А.Г. Купцов: Миф о гонении церкви в СССР
• Б. Вишневский: Поповизация УК РФ
• Библейские персонажи
• Бескорыстие православной церкви
• Ленин приказал расстреливать попов
• Был ли Иисус неевреем?
• Главный поп всея Руси рвётся в поп-звёзды
• Смерть православия
• Как РПЦ во главе с Гитлером воевала против советского народа
• 5 лет за свободу совести
• Сергиев Посад. В логове зверя
• Путлеровцы посадили за экстремизм Л.Н. Толстого
• Путлер: за атеизм тюрьма
• А.Г. Невзоров: Отставка Господа бога
• Раввин Иисус был агентом древнеримской охранки?
• Православный космос, или вместо экспериментов молитвы
• Как христиане любят ближних
• Кому и чему молятся православные?
• В. Орлов: РПЦ изнутри
• Святые отцы РПЦ
• УК царизма: как нагайками вколачивалось православие
• Невежественность профессора Осипова
• Туринская плащаница
• Поповские мифы
• С.Л. Толстой: как РПЦ уничтожала духоборов
• А. Невзоров: Гомосексуализм цементирует РПЦ
• В США зверски убивают атеистов
• Православный террор РПЦ
• РПЦ сажает конкурентов
• Во имя господа Иисуса Христа! Огонь!
• Православная эксплуатация человека человеком
• Кто такие святые?
• За что большевики попов убивали
• Противоречия в Библии (торе)
• Нелепости учения о Христе
• Церковь и наука
• А. Невзоров: Иисус Тангейзерович Чаплин
• Соглашение Минздрава РФ с РПЦ
• Как РПЦ оккупировала Соловецкие острова
• Скромная яхта Путлеарха
• Духовные скрепы
• ШизоНаркоЭксперт РПЦ Дворкин
• Поп Чаплин: гомосексуализм это награда VIP-попов
• Иисус разрыватель детишек медведями
• ФСБ занялось атеистами
• Иегова-Иисус увольняется за профнепригодность
• Патриарх — просветитель пингвинов
• Резьба по клитору - духовная скрепа
• Наше спасение в рабстве у Путина
• Попы РПЦ и Поклонская о Николае Втором
• РПЦ и власть. Хроника любви
• Исповедь бывшей послушницы
• Про дела церковные
• Православный терроризм Поклонской
• Групповые изнасилования по-православному
• Расследование о детях-невольниках в РПЦ
• Как РПЦ зарабатывает миллиарды
• Православные зэки
• Коммунист-атеист-православный буржуй Валя Терешкова
• Попы побратались педерастами
• Бесы Владимира Соловьева
• Молебен ВЦИОМ за правильный опрос о храме
• Черти в рясах РПЦ
• Деньги во славу Божию. Как финансируется РПЦ
• Миллиардер Гундяев против стяжания!
• Буржуйский поп Зюганов
• Конкурс мракобесия
• 7,5 лет за богослужения
• В тюрьму за веру
• Докинз - снова еретик
• Ананас веры
• Происходит изобретение "традиций" задним числом
• Как очистить ДНК от невежества

Статистика

Пользователей
Статистика
  • Всего сообщений: 9402059
  • Всего тем: 70797
  • Онлайн сегодня: 361
  • Максимальный онлайн: 6088
  • (07 Октябрь 2015, 10:58:05)
Сейчас на форуме
Пользователи: 8
Гостей: 218
Всего: 226

О. Поливанов

• Террор, как метод революционной борьбы в РФ.
• Революционная стратегия коммунистов
• Фашистский Кремль опять арестовал полковника Квачкова
• А. Соулдженайсен: Один день Воруй Воруевича
• Л.Н.Худой: Оборзение
• Рецессивный атавизм постсоветской России
• Кто такие евреи?
• Пожар в ухтинском универмаге как символ буржуазного права
• Сталинские репрессии. Жертвы коммунистического террора.
• Власовская удавка для Лундина и Романова
• Тайна СШ-катастрофы, или борьба с терроризмом по-Путински
• Простая суть коммунизма
• Путин и Медведев испугались революции
• Надо ли ходить на выборы?
• США как детонатор мировой социалистической революции
• Почему США официально признали чуровские подсчёты?
• Современная РПЦ
• Герои нашего времени: русский патриот Ю. Буданов
• Почему Сталину ставится в вину то, за что возвеличивается Кутузов?
• Донцова-Отец: Три путлераста
• Танки били по верховному совету РСФСР из 1983
• Золотой свинёнок
• Список Спилберга: фильм
• Православное преступление и патриаршее наказание
• Э. Володарский: Евангелие о Чапае
• Мыся Пурим: Культурная яма
• Как ЦРУ спасало жизнь Джеймсу Кэмерону
• Батрак Абрама: Абу-Грейб Гуантан, агент 911
• Владимир Путлерович: Москва 2032
• Как Ленин делал революцию на немецкие деньги
• Как Италия промышляет работорговлей оппозиционерами
• Как Путин сжег самоуправление Ярославля
• Обращение в прокуратуру о принуждении к православию
• Героизация бородатой сволочи
• Постсоветский кинематограф
• Христиане
• Уничтожение советской киноклассики
• Евангельские рассказы для детей
• Тайна смерти А. Меня и Ю. Семёнова
• Банальная тайна убийства М. Евдокимова
• Как умер Стенли Кубрик
• Ю.Андропов, - конец лжи
• Теория большого маразма
• Перстень Борджиа для Леонида Филатова
• Проституция Никиты Белоголовцева
• Хелен Мирен в травле Льва Толстого
• Крым с Р.Ф. Что дальше?
• Письмо президенту РФ о лунной афёре NASA
• После Крыма путлеровцы решили одеть на россиян кляп
• Политическая цензура поисковиков
• Что ждёт РФ в ближайшем будущем
• За что убили актёра Андрея Панина?
• Интервенция Путина на Украину
• Почему фашисты в Москве, а не в Киеве
• Культурная армия Путина
• О легитимности кремлёвской хунты
• Почему не наказаны убийцы Литвиненко?
• Единство Четвёртого Рейха
• Вова Сорокин как зеркало постсоветского маразма
• Крокодиловы слёзы Путина
• 1 Мировая. Путинский плачь по империализму
• Ложь о паспортной системе СССР
• Эпидемия фашизма у обывателей РФ
• Крёстный тесть
• Путлерюгенд и информационное гестапо РФ
• Бастрыкин выкинул с 6-ого этажа генерала МВД
• От чего умер Ельцин?
• Путин душит независимое ТВ
• Рейхсминистр пропаганды Лимонов
• Как фейсбук спамит нам мозги
• Иллюстрация к безальтернативности коммунизма
• Демографический прогноз Д.И. Менделеева
• Православный мир на Украине
• СССР. Нефть. Миф о падении цен
• Ещё раз о еврейском народе
• Власовская тряпка кремлёвской хунты
• Историческое враньё с Николаем Сванидзе
• Казанский Боинг ещё один скрытый теракт
• Дело Тихонова, Хасис и Горячева наш троцкистско-зиновьевский центр
• Беда Исраэля Шамира
• Свобода гадить на ислам
• Сытая отрыжка Говорухина
• О личности политического лидера. Б.Немцов
• ЦРУшные взрывы в Бостоне и фабрикация дела против Царнаевых
• Протоиерей Чаплин: православие это дикая злоба
• Как кремль заметает следы убийства Немцова
• Путлевизор
• Кто стоит за парижскими атаками 2015?
• Пророчество советской пропаганды
• Кто, если не Путин?
• О роли идеологии
• Календарные мифы
• Как Ленин в 1922г. попов стрелять призывал
• Лунная точка зелёного кота Егорова
• Физический прокол Стенли Кубрика при съёмках лунных миссий в павильоне
• Глобальное потепление такая же ложь, как ОМП в Ираке
• Цель закона Яровой тотальная слежка
• Путин готовит переворот?
• Любовь к Путину
• Как Путин врёт про Боинг
• Людей или автоматику легче высадить и забрать с Луны?
• Ельцинские мифы
• Шитая белыми нитками «тайна» убийства Джона Кеннеди
• Трамповская буря в вашингтонском стакане
• Информационное Гестапо Путина
• Фашизм и нацизм
• О плановой и рыночной экономиках
• Светоч демократии и верховенства права
• Что такое Биткойн
• Путин прячет детские трупы ТЦ «Зимняя вишня»
• Цензура коммуниста remi-meisnerа
• Пара слов в защиту Судоплатова
• Реабилитация Чикатило
• Гонения на Аум Синрикё или великомученик Асахара
• Хахалесудие
• Рэмбо из Керчи Росляков
• Разгадка тайны гибели группы Дятлова
• Буржуйская мораль
• Гонения на неверующих в буржуйской России
• В России репрессируют не только неверующих, но и верующих инако
• Формы антикоммунистической борьбы
• Как сестрички Хачатурян правосудие насиловали
• Как в России расследуют убийства детей
• Климатический фашизм
• О том, как Евгений Манюров ФСБ расстреливал
• О детском сексуальном рабстве
• Короновирусный психоз правительств
• Цель коронафейковой паники опустить Китай
• ДТП Ефремова спецоперация ФСБ
• Общие выводы теории относительности
• Время и пространство
• В поисках божественного
• Суть дифференциального и интегрального "чуда"
• Сталинская контрреволюция
• Общая теория поля
• Когда снова начнут взрываться жилые дома?
• Справедливость русского мира
• Так кто взорвал Крымский мост?
• Битва русских рабов за своё рабство
• Физика чернобыльского взрыва
• Роль Луны в жизни землян и инопланетяне
• Один пример бреда современных "квантовых механиков"
• Зачем Путин убил Навального?
• Навальный жив, и передан Путиным США!
• Проблема закона сохранения энергии в квантовой механике
• Как США и Путин утопили "Курск"
• Что такое электрический ток?
• Мюнхенский сговор 2.0 закончится Мировой войной 3.0
• Почему возникло христианство?
• Как Теорию Относительности объяснить без релятивизма

Экономика и финансы

Великая, могучая Омэрика…
• Капитализм - это действительно дерьмо!
• Помойное изобилие и крах сельского хозяйства.
• В.М. Кузнецов, руководитель рабочей группы по борьбе с коррупцией при Государственной Думе РФ: Доклад
• Будзилович П.Н: Битва кагала за финансы антихриста
• В.М. Кузнецов, руководитель рабочей группы по борьбе с коррупцией при Государственной Думе РФ: Второй Доклад
• В.С. Волков: Так живет рязанская глубинка
• Население России. Статистика, факты, комментарии, прогнозы
• В.М. Кузнецов: 3 Доклад о коррупции
• Россия в цифрах
• А. Сёмин: Село в России идет на эшафот?
• Д. Бутрин: Зарплаты иностранцев в России
• А. Полухин: За восстановление электросетей заплатит население
• Путин. Коррупция. Независимый экспертный доклад
• Власть Семей. Президент. Часть 1.
• С. Дунаев: В хранилищах США вместо золота лежит вольфрам?
• С. Канев: ОПГ «Кремль»
• З. Бурская: Воровской общаг администрации Президента РФ
• А. Брусилов: Царская Россия в цифрах накануне Первой Мировой
• НЕ Официальная статистика
• Ю. Мухин: Врать про мясо как Путин
• В. Наганов: Путинские экономические заслуги
• Снижение оплаты ЖКХ в обмен на поддержку ПЕДИРосс
• Коррупция в МИДе, открытое письмо
• Немцов: золотые галеры Путлера
• Офигенный российский бизнес…
• Путин. Итоги
• Рабский секрет китайского экономического чуда
• Цветы изобретателю столыпинского галстука
• Буржуазные знахари ЕС
• Где хранится золото мира?
• 12 мифов о капитализме
• 1% россиян владеют 85% богатств страны
• Мировой капиталистический ГУЛАГ
• Власть Семей-2011. Премьер и его круг
• Дома друзей Путина
• Рубль и Путин
• А. Кунгуров: Нефтяная смерть Путина
• А. Кунгуров: КтоЕслиНеПутин?
• А. Кунгуров: Антикризисный план правительства – гон обгашенных нариков
• Уральский срез
• А. Кунгуров: Диагноз окончательный – смерть!
• Украденное Сердюковым переоформляли на соратника Путина
• А. Кунгуров: План Путина
• А. Кунгуров: экономические итоги РФ к 2016г.
• А. Кунгуров: Бриллиантовый мародёр Нахалков
• А. Кунгуров: Как победить кризис. Рекомендации Сталина
• Только за 2005-2011 кремлёвская хунта украла у РФ 1 триллион $
• Кормит ли Россия сама себя, как утверждает Дмитрий Медведев?
• Экономические достижения Ельцина-Путина
• Достижения ПЕДИРосс
• С. Демура: в РФ будет коллапс
• Экономические итоги 2016
• Пять лет со дня расстрела рабочих Жанаозена
• А. Кунгуров: Подарок Сечина самому себе
• Кунгуров о росте экономики РФ
• Эффективные манагеры
• Капитализм с человеческим лицом
• Космическое мародёрство Кремля
• Путин это победа!
• Крах эпохи социального государства
• Гримасы капитализма
• Помойная экономика капитализма
• "Дисфункции" капитализма Глазьева
• Колхозы при капитализме норма
• Укронадежды
• Эффективные бизнесмены против неэффективных россиян
• "Коммуналка" для Новой Нефти
• Медицинское-интернациональное
• Всерьез о Сталине
• Расслоение населения по доходам сейчас выше, чем в начале нулевых
• Высокотехнологичный экспорт в СССР
• Окончательное ниспровержение марксизма ч.1
• Окончательное ниспровержение марксизма ч.2
• Россия вымирает с рекордной скоростью
• Скулёж Атлантов
• Наивное буржуйское желание выжить
• Коронавирусная паника устроена фармкомпаниями
• Коррупция в ВОЗ
• Как правильно пугать COVID-19
• РежЫм против Короны
• Поддержим Нацлидера!!!
• Капиталистическое пепелище Путина
• Ваша нищета гарантирована Путиным
• Руины белорусской экономики Лукашенко
• Битва ключевых технологий США и Китая
• Что и сколько стоило в СССР
• Россия начинает признавать действие санкций
• Газовая победа Путина
• Удивительно, — рубль рухнул, и вдруг все подорожало!

Иудаизм

• В. Бёрд: Аушвиц, окончательный подсчёт
• И. Брумель: Надо ли верить в холокост?
• М. Хрусталев: Холокост множит антисемитов
• В. Иванов: Бабий яр
• Место «самых умных» евреев в конце списка призёров математических олимпиад!
• Политическое влияние еврейства на постсоветском пространстве
• Е. Лобков: Евреи пишут письмо Сталину
• Д. Асламова: Палестинский холокост
• А Эвентов: Страна победившего расизма
• Еврейство на экране. Фильмы и ролики
• В школах РФ будут преподавать Холокост
• Еврейская армия Гитлера
• ООН запретил репрессировать неверующих в Холокост
• Иудейское христианство
• И. Слисаренко: Карикатуры на Мухаммеда, - свобода слова, карикатуры на холокост, - антисемитизм!
• ЕС заставляет изучать Лохокост все страны мира
• Еврейский след в нью-йоркском теракте 9/11
• Израиль открыто готовит бандитов и террористов
• Почему в Освенциме не нашли евреев?
• Еврейские банды Второй мировой
• Нюрнберг о холокосте
• Разоблачена очередная жертва холокоста
• Холокост Стивена Спилберга
• Симон Визенталь - фальшивый охотник за нацистами
• Как Израиль сотрудничал с SS
• Об ужасах холокоста
• Сколько и как убивали евреев
• Юрген Граф: Ревизионизм холокоста
• Религия холокоста
• Холокост, не дай себе засохнуть!
• Жертва еврейско-канадского ГУЛАГа
• Отзыв млн. бракованных холокостнутых евреев
• «Гитлеровец» для израильтянина - похвала
• Коррупция холокоста
• Оборотни холокоста
• Хамы лохокоста
• Как Израиль уничтожал расово-неполноценных
• Рассказам о холокосте 200 лет
• ИГИЛ дело рук Израиля
• Еврейское Гестапо ФРГ
• Подлинник «Протоколов сионских мудрецов»
• Новости антисемитизма

Наука и образование

• И. ДЬЯКОВ: Уничтожение российских учёных.
• А. Дальский: Американцев не стояло на Луне
• Вакуумный Клондайк РАН и РПЦ
• Православное изнасилование МИФИ
• Кафедра теологии МИФИ: о сотворении мира (конспект)
• Учреждение кафедр мракобесия во всех ВУЗах РФ
• Учёные потребовали доказательств байки про чудесную крещенскую воду
• В России вводится платное среднее образование
• Поповская биология в школах
• Из МИФИ увольняют атеистов
• Научные ахинезаторы МГУ
• Лунная база
• ВАК центр индустрии фальшивых диссертаций
• Расчет доз радиации Аполлонов
• О поддельных лунных снимках LRO
• Голливуд на Луне и до нее
• Уничтожение образования в РФ
• Интервью С. Кубрика: я участвовал в лунной афёре NASA
• Л-к С. Савицкая на службе NASA и ЦРУ
• Чернобыльская катастрофа
• Цензура вопросов о лунной легенде NASA
• А. Попов: Бодряки с «орбиты». (факты и версии)
• Фальшивый цвет американской «Луны»
• 1975 г., ЭПАС: «Союз» летал, «Аполлон» - нет!
• «Звёздная слепота» NASA
• Влияет ли вранье NASA на зрение?
• Остап Петрикович Маск или Илон Мавродиевич Петрик
• Воспоминания ракетчика
• Православный талибан РАН
• Снова о Сатурне-5 и конусе Маха. А.И. Попов был прав!
• Про американские лунные выходки
• Путь фон Брауна в тупик
• Антинаучная диссертация Мединского
• Как наши следили за американцами на Луне
• Лунные фотошоперы NASA
• Реальные метеориты на голливудской Луне NASA
• О лунных фотографиях NASA
• Миф Аполлонов
• Почему все кадры с Луны не далее 19 метров? ч.1
• Почему все кадры с Луны не далее 19 метров? ч.2
• Почему все кадры с Луны не далее 19 метров? ч.3
• Шариков истинно свидетельствует о полётах на Луну
• Путин космически обделался
• О верующих учёных
• Самые заметные проезды NASA по бутафорской Луне
• Как должны выглядеть движения астронавтов на Луне?
• Неопровержимое доказательство высадки на Луну
• Леонов врёт про лунный автограф астронавта Сернана
• Сколько раз соврал космонавт-банкир Леонов?
• Что знали советские специалисты об американских полётах на Луну?
• Мюнхгаузен действительно летал на Луну!
• Учёные установили фальшивость лунных камней NASA
• СССР не следил за полётами Аполлонов ч 1
• СССР не следил за полётами Аполлонов ч 2
• СССР не следил за полётами Аполлонов ч 3
• В МГУ состоялось заседание мракобесной ассоциации
• Как СССР устроил двойную засаду на Аполлон-13
• Документов по слежению за Аполлонами в СССР нет!
• Рецензируемые научные журналы публикуют фейки
• Кто вместо Армстронга спускается по лесенке?
• Купить книги д-ра физ.-мат. наук А.И. Попова о лунной афёре NASA
• Действительно ли происходит глобальное потепление?
• Ложь NASA о серой Луне добралась до глобусов
• Google: запрещает сомневаться в полётах на Луну
• Шаттлы – шумный старт и тихий финиш
• Станция Скайлэб никогда не была в космосе
• Академик РАН: Человечество ждет новый ледниковый период, а не глобальное потепление
• Надо ли бояться углекислого газа в атмосфере?
• Так давали ли СССР американцы лунный грунт?
• Про фотоплёнку и радиацию в космосе
• Большой ученый Путин
• Одиссея капсулы Аполлон-13

18 Май 2021 - • Суть дифференциального и интегрального "чуда"

Автор Админ 18 Май 2021, 17:15:00 13437 просмотров Рейтинг: 0 (0 Оценки)
• Общие выводы теории относительности
• Время и пространство

Автора статьи с первых уроков дифференциального и интегрального исчисления до сего дня не оставляло чувство недосказанности, а сам метод казался висящим в воздухе. Куча вопросов остаётся без ответа. Создаётся впечатление, что суть этого метода мало кто понимает до сих пор, но религиозная точность придерживания канону позволяет обходиться и без него. Нам же хочется полного и абсолютного осмысления вдоль и поперёк. Это совершенно иное, нежели запоминание и повторение соответствующих разделов учебников математики.   
Иоган Кеплер придумал оригинальный способ расчёта площади круга "на коленке". Он разбивал его на сектора, число которых предполагалось как угодно большим, так что площадь каждого стремилась к нулю. Бесконечно малый сектор имеет такое бесконечно малое основание, которое, будучи куском дуги превращается в прямой отрезок. 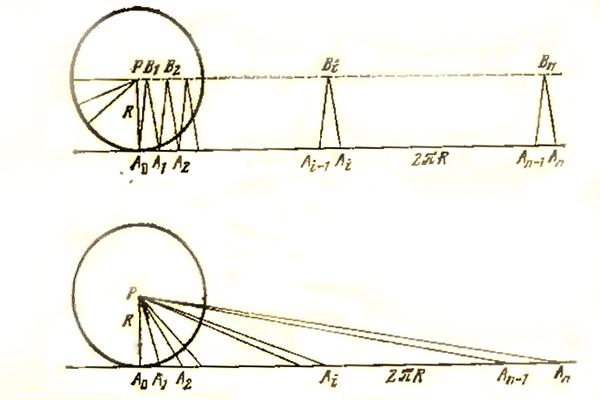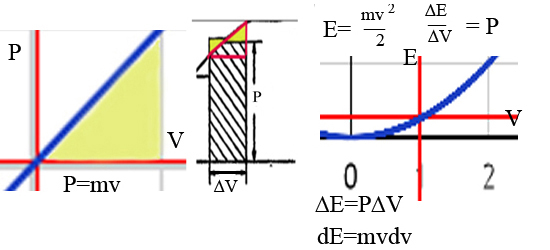Затем он мысленно составлял из этих секторов прямоугольный треугольник с большим катетом 2R и высотой R. Каждый бесконечно малый сектор из круга был равен бесконечно малому своему эквиваленту в треугольнике, поскольку площадь треугольника это произведение полувысоты на основание. (Остроугольный треугольник сектора равен площади тупоугольного треугольника своего эквивалента, высота которого далеко выходит за пределы самого треугольника, так как равны их основания и высоты.) Посчитать же площадь большого треугольника не составляет труда. Мысленной заменой криволинейной фигуры, площадь или объём которой мы не можем посчитать в лоб, на простейшую площадь или объём, мы получаем возможность узнать их. Интегральный метод это способ такой трансформации для любой подобной задачи.

Допустим, что нужно найти объём шара. Мысленно расчертим поверхность шара бесконечно большим количеством меридианов и параллелей. Бесконечно малая ячейка этой сетки станет основанием пирамиды с вершиной в центре шара. Стремление площади основания такой пирамиды к нулю позволяет считать его плоским. Объём любой пирамиды вычисляется как треть произведения его площади основания на высоту. Значит, суммирование объёма всех пирамид получившихся в результате разбиения, даст то же соотношение для полного объёма шара, - треть произведения площади поверхности шара на его радиус V= SшR/3. Теперь представим себе конус с основанием равным площади поверхности шара, и высотой равной радиусу шара. Он будет равен объёму шара. Мы можем вычислить "на коленке" одну величину, имея другую (объём шара или площадь его поверхности). Но какую-либо из них нужно найти иным путём.

Для того, чтобы посчитать объём любого тела, например, шара мы помещаем его центр в центр нашей системы координат. X будет скользящая вдоль оси абсцисс точка перпендикулярного ей сечения шара, становящаяся тем самым центром этого сечения. Для вычисления площади сечения мы используем теорему Пифагора. Записав площадь через X в общем виде, мы получили все возможные сечения. В плоской системе координат это перевёрнутая парабола пересекающая ось абсцисс при X = +/-R. Каждой абсциссе теперь соответствует ордината, являющаяся площадью сечения, а все вместе сечения, которые мы называем бесконечными, образуют объём шара. Таким образом объём стал площадью под кривой, и вывод об этом мы сделали в рамках простых логических рассуждений. Все возможные сечения заключены под кривой, и там нет никаких лишних сечений. Мы "берём" математическую "палку" и последовательно "прикладываем" её к "удаву" выясняя какому количеству черепах он равен. Помогли нам в этом декартова система координат и знание площади круга, позволившая записать в общем виде формулу площадей сечений для любого X. Шар теперь создаётся движением сечения по закону окружности. Мы абстрактно задаём фигуру при помощи формулы, потом переводим её в другую такую же абстрактную фигуру попроще, и в конце концов получаем самый простой вид абстракции. Для того, чтобы появилась площадь поверхности и объём фигуры, мы должны их вырезать из единой реальности, "оцифровать" формулами.

При таком подходе нам даже не понадобилось бесконечно складывать бесконечно малые. Теорию о бесконечно малом и большом мы развиваем уже исходя из этого переноса, чтобы его прокомментировать.

Бесконечно-малое и бесконечно-большое

Понятие бесконечно малого в корне отличается от просто очень маленького числа. Важным свойством поля вещественных чисел является выполнимость в нём аксиомы Архимеда: если имеются два отрезка a и b, причем a меньше b, то взяв a некоторое количество раз можно превзойти b. С бесконечно малым этот принцип не работает, - сколько n раз не бери бесконечно малое, оно не превзойдёт никакое сколь угодно малое вещественное число. Но если его взять бесконечное число раз, бесконечно-малое обретает вещественное протяжение.

Бесконечное множество отличается от любого самого большого числа тем, что невозможно назвать "сколько это в цифрах", а это возможно только при одном условии, - численность такого множества меняется, и меняется в сторону увеличения с бесконечно большой скоростью, никогда не прекращая рост. Изгибающаяся на графике функция в каждой точке своей кривой имеет строго определённый наклон к осям координат. Если у точки обозначающей этот наклон есть реальная протяжённость в пространстве, между ней, и точкой находящейся рядом, должна быть строго определенная граница. Но между двумя какими угодно близкими точками мы всегда можем всунуть бесконечное их множество. Значит, границ у бесконечно малых точек нет, поэтому нет и реальной вещественной протяжённости. Хотя у такой точки есть наклон и "центр" обозначающий её место на оси координат. Суммирование всех бесконечно малых, бесконечно возрастающих в числе, не имеющих никакой вещественной протяженности точек, составляющих вещественный отрезок, даёт нам реальную протяжённость. Вот какими рассуждениями мы приходим к понятию бесконечно малого.


1. Все согласны с тем, что на любом отрезке можно разместить бесконечно много бесконечно-малых.
2. Если мы разделим этот отрезок на бесконечно много частей, длина каждой такой части будет равна нулю, так как деление числа на бесконечность даёт ноль.
3. Если мы разобьем на бесконечное число частей два отрезка, один из которых будет длиннее другого вдвое, то у каждого бесконечно малого отрезка в результате разбиения длина будет равна нулю, но длина равная нулю большего отрезка будет в два раза превосходить равное нулю бесконечно-малое меньшего отрезка. (Именно поэтому деление на ноль неопределённость. Ноль это бесконечно-малое, которое может иметь какое угодно значение.)
4. Если мы плавно изогнём отрезок, каждая его точка изогнута не будет, так как она не имеет вещественного протяжения. Но изгиб присутствует физически, а вещественное существование отрезка обеспечивает бесконечное множество бесконечно-малых. Значит, изгиб должен затрагивать все бесконечно-малые, наклоняя их подобно звеньям цепи под действием силы тяжести, и каждое бесконечно-малое будет иметь свой наклон, отличный от соседнего. Таким образом, бесконечно-малое не имея вещественного протяжения, имеет ориентацию в пространстве.

Приведём практический пример пользы от этой "эквилибристики", посчитав площадь круга, составив из секторов на этот раз не треугольник, а параллелограмм или трапецию, соединяя сектора "вершина к основанию", словно всовывая зубья одной пилы в зубья другой. Поступим так со всеми секторами и соединим параллелограммы. У нас получится фигура с двумя параллельными сторонами равными R и двумя сторонами равными R. Как мы знаем, её площадь должна быть равна R2, а это значит, что параллелограмм прямоугольный, то есть высота равнобедренного треугольника (бесконечно-малого сектора) равна двум его сторонам. У сектора ставшего треугольником вершина и основание оказываются безразмерными, равными нулю точками, но за счёт бесконечного суммирования оснований они обретают протяжённость. Точки вершины треугольников-секторов - центр круга, будучи единственным на все треугольники-сектора, не суммируется в протяженность, оставаясь невещественной точкой. В результате наших мысленных экспериментов с превращением пространства в нуль и обратно в пространство мы реально решили довольно сложную задачу! Бесконечно малое равно нулю и оно же "в потенции" от него отлично. Если сектор круга отличен от нуля, то дуга не полностью выпрямиться, и при суммировании мы потеряем часть площади круга. Если сектор равен нулю, то, сколько бы мы не складывали нули, ничего кроме них мы не получим. Следовательно, под бесконечно малым мы должны понимать некую среднюю, отличную и от нуля и от какого-либо протяжения величину. Мы продифференцировали круг, потом проинтегрировали и получили площадь. Эти приёмы неосуществимы в физическом мире, так как очевидным образом в его логике абсурдны. Математическую же логику они не нарушают.

При интегрировании подсчитывается бесконечная сумма площадей прямоугольников с бесконечно малым основанием и высотой равной ординате функции в этой точке. Верхушкой этого прямоугольника обычно является наклонённое под разными углами бесконечно малое, то есть некоторый треугольник. Если мы прочертим через середину гипотенузы линию, параллельную основанию этого прямоугольного треугольника, она разрежет другой катет тоже ровно пополам. Образуются два равных треугольника, один под чертой, участвуя в подсчёте общей площади, другой над, - не участвующий. Нижний в точности компенсирует верхний. Таким образом, никаких потерь или излишков при подсчёте интегральной площади не происходит. Выражения "пренебрежимая малость", "приближенность" описывающие этот момент в учебниках математики, вводят в заблуждение. 

Интегральный метод расчёта процессов

Возьмём функцию y=x и построим на её основе другую функцию по определённой закономерности - ордината Y при той же абсциссе X на втором графике должна быть числено равна площади, отсекаемой на первом графике абсциссой, графиком функции, и перпендикуляром, установленным в точке X. Эта площадь будет половиной квадрата со сторонами X. В общем виде получаем функцию y=x2/2. Назовём первую функцию производной, а вторую первообразной. 

Какую бы точку второй функции мы не взяли, ей соответствует площадь на первом графике. Если мы на втором графике берём две соседние точки, то та точка, что расположена правее, имеет эквивалент площади чуть больший, чем точка левее. При этом отображение Yпроизводной - Yпервообразной и обратно происходит с помощью прямого и обратного коэффициента х/2. (Площадь под кривой для степенной функции пропорциональна степени. Для x2 это 1/3 (установлено ещё Архимедом), для x3 1/4, для xn 1/(n+1). Это требует отдельного и пространного доказательства.) Отсчёт нашей производной мы вели от начала координат, но можем задать любой интервал на оси абсцисс и получить результат, в том числе отрицательный, если площадь находится под осью абсцисс производной.
(На чертеже две соседние точки, приближаясь, друг к другу сливаются в касательную.)

- Возьмём на первом графике две соседние, не имеющие между собой вещественного расстояния точки X-X0=∆X, и опустим из них перпендикуляры на ось абсцисс. Получится столбик с невещественной площадью ∆s, который, по условиям договора будет иметь на втором графике невещественный эквивалент в виде отрезка Y=Yпервообразной-Y0первообразной.
- Разбиваем первообразную кривую на точки, каждую из которых рассматриваем прямой, и поступаем с ней, словно она линейная функция нулевой протяженности, назвав касательной. Тем самым мы перешли от двух соседних точек к одной точке с двумя краями невещественной протяженности по соответствующим осям Yпервообразной и гипотенузой, являющейся прямолинейным куском функции или касательной к графику Y=x2/2 в точке X.
- Так, как площадь прямоугольника на первом графике ∆s=∆Yпервообразной второго графика, основание его равно ∆X, то высота прямоугольника получается ∆s/∆X, или что то же самое, ∆Yпервообразной/∆X, а это тангенс угла наклона касательной к оси абсцисс первообразной, или значение графика производной функции в этой точке, то есть в данном случае Yпроизводной при нашем X. "Кривизна" первообразной переходит в ординату производной. Отсюда известное определение: значение производной функции в точке равно тангенсу угла наклона касательной к оси абсцисс первообразной в этой точке. Получив его, мы можем построить из первообразной функции производную, и из производной первообразную, умножением на прямой и обратный коэффициент.   

Сказанное выше сформулировано в учебнике математики так:  f`(x)=lim∆f(x)/∆x
                                                                                                         ∆x->0
Производной функции f`(x) равен предел отношения приращения этой функции к приращению аргумента, когда приращение аргумента стремиться к нулю.

Показательно можно наблюдать связь между производной и первообразной через геометрию. Представим функцию f(x)=x2 как площадь квадрата со стороной x. Нарастим стороны на dx, тогда приращение площади df=xdx+xdx=2xdx (произведение бесконечно малого на себя dxdx даёт ноль) откуда df/dx=2x будет скоростью нарастания площади при увеличении стороны, то есть производной.

Как видно, это тот же самый кеплеровский приём мысленного разбиения на бесконечно-малые с последующим сложением, расширенный для любых фигур до универсального.

При интегрировании и дифференцировании функция обычно меняет свою форму, но есть функция, которая её меняет в свою же собственную. Если исходная сумма $1 и начисляется 100% годовых один раз в конце года, то итоговая сумма будет $2. Но если те же самые проценты начислять два раза в год, то $1 умножается на 1,5 дважды, получая $ 1,00*1,52 = $2,25. Начисления процентов раз в квартал приводит к $1,00*1,254 = $2,44140625, и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел:
lim(1+1/n)n=e=2,718 28……    Функция вида ex и будет той магической функцией, которая
∆n->∞
описывает в природе радиоактивный распад, когда из некоего числа радиоактивных ядер за время T распадается строго половина. А потом из той половины за это же время распадается снова половина. И т.д. N = Nое-λt где Nо начальное количество ядер, а N через время t. Так происходит потому, что у функции ex площадь под ней от начала координат до любой абсциссы в точности соответствует ординате этой абсциссы. Тогда тангенс угла наклона касательной в любой точке равен значению её же ординаты. Когда площадь под какой-либо функцией от начала координат до некоторой абсциссы больше или меньше значения соответствующей ординаты, ордината этой абсциссы на графике первообразной тоже становится больше или меньше. 

Разберём работу метода на примере расчёта объёма шара.


Мысленно разбиваем шар на бесконечное количество сечений, и находим функцию, которая описывает изменение площади этих сечений. (Начало координат помещено в центр шара.) Радиус окружности, мысленно движущейся от одного края шара через центр к другому, рассчитывается через теорему Пифагора – корень квадратный из разности квадратов радиуса шара и квадрата х – расстояния центра "движущейся" окружности до центра шара. Искомая функция - изменяющаяся площадь "движущегося" круга. В итоге получаем перевёрнутую параболу S(х)= (R2-х2), огораживающую над осью Х площадь (площадь площадей сечений шара) - искомый объём шара (2R32/3=4R3/3 Расчёт методом Архимеда). Каждое значение Х это конкретное значение площади соответствующей ему окружности (Y), а все вместе они образуют площадь в точности эквивалентную объёму шара. 


Чтобы посчитать общую толщину не имеющих толщины двумерных площадей, то есть площадь под параболой (R2-х2) интегральным способом, используя наш договор о двух графиках, находим функцию, которая переводит всю искомую двумерную площадь в одномерный отрезок по ранее условленному принципу. Измерение отрезка даёт нам искомую площадь (в данном случае объём). 

Проанализируем последовательность действий, приводящую к интегральному "чуду"
1. Устанавливаем соответствие между площадью сечения шара и ординатой (длиной отрезка) функции S(х)=(R2-х2) при любом Х. 
2. Чтобы посчитать площадь под параболой, находим функцию, которая переводит всю искомую двумерную площадь в одномерный отрезок по ранее условленному принципу. Измерение отрезка даёт нам искомую площадь, - в данном случае объём.   

Мы приравниваем объём шара как целого, целой и нераздельной площади под кривой, потом приравниваем её к единому и неразрывному отрезку, длинной которого становится искомый объём. Без всяких бесконечно малых. То, что в интегральном методе расчёта "захотела природа" выражается кривой, описывающей исследуемый процесс нарастания площади кругов по мере продвижения к центру. Остальное лишь условность.         

Остаётся найти дифференциально-интегральную связь разных функций, доказать что, например, производная синуса есть косинус, чтобы расширить интегральный метод на все функции. И ещё кое-какие мелочи. Интегрирование это нахождение функции, связанной договором с имеющейся функцией о равенстве площади под кривой ординате искомой функции. Интегрирование позволяет  рассчитывать суммарный итог непостоянного изменения.

Дифференциальный метод расчёта процессов

Бесконечно малое приращение радиуса шара, равное во всех направлениях от некоего центра даёт одно и то же во всех направлениях приращение объёма, который соответствует строго определённой площади. И это очевидное тройное соответствие мы можем взять в качестве доказательства работающей дифференциально-интегральной связки S=∆R/∆V. (Кстати вот зримый пример соотношения двух равных нулю величин, дающего в итоге вещественную величину.)

Найдя объём, мы получаем площадь поверхности шара из нашей формулы, добытой "на коленке" V= SшR/3, приравнивая объёмы шара и пирамиды высотой равной радиусу шара, с основанием равным площади его поверхности. Тот же результат мы можем получить, если сделаем переменной радиус шара и продифференцируем по нему формулу его объёма. V`=(4/3)х3dx= 4х2=Sш
Площадь поверхности шара — это скорость изменения его объёма. Так произошло потому, что переменная, в роли которой выступает радиус, всегда строго перпендикулярна тому бесконечно малому и потому плоскому кусочку поверхности шара, до которого радиус проводится, а радиус одинаков по всем направлениям. Любой бесконечно малый кусок поверхности шара является касательной плоскостью к радиусу. (То же происходит с кубом, если его объём записать формулой переменной в которой будет расстояние из центра куба до его граней: Vкуба= (2х)3, где х половина ребра куба. Тогда Sповерхности=2х*2х*6=V`куба=(2х)3dx=8*3х2=24х2) Если мы возьмём полусферу, половину куба, дифференциально-интегральная связь объёма и площади поверхности разорвётся. Пропорциональность приращения во всех направлениях объёма к приращению площади нарушается. При анализе соотношения площади поверхности и объёма шара, куба, правильного икосаэдра соотношение их объёмов и площадей поверхности, записанных через радиус вписанной сферы - 1/3, а это ещё и коэффициент дифференцирования описывающей объём степенной функции. Производная объёмов перечисленных фигур, записанных через радиус вписанной сферы, равна соответственно площадям их поверхностей записанных так же. Аналогичное соотношение 1/3 площади поверхности к объёму у правильного тетраэдра, но приращение площади поверхности и его объёма не во все стороны от центра равномерно, поэтому интегрально-дифференциальной связи между объёмом и площадью не наступает. 

Нестрогое, но наглядное объяснение было в школьном учебнике под редакцией Колмогорова. Представим себе, что мы покрыли поверхность шара тонким слоем краски равной толщины. Приращение объёма шара - это объём израсходованной краски ∆V. Делим его на толщину слоя краски - на приращение радиуса шара. Получаем, что площадь S поверхности шара - это отношение ∆V/∆R - тангенс угла наклона первообразной, где ∆R мало. Если радиус шара увеличить на ∆R то объем шара увеличится на ∆V, причем приращение объема равно дифференциалу (от лат. differentia «разность, различие») объема ∆V=S∆R. График первообразной показывает нам, какой объём шара будет при заданном R(х), а угол наклона касательной в этой точке покажет, чему будет равна при этом площадь шара. График производной показывает нам, какую площадь приращений под параболой нужно просуммировать, чтобы она равнялась своему объёму на графике первообразной, и как меняется площадь поверхности шара, выраженная ординатой в отношении к отсекаемой площади под кривой, символизирующей изменение его объёма.
Чтобы понять символизм записи снова вернёмся к подсчёту площади круга. Разобьём его на множество бесконечно малых колец. Тогда площадь любого из них будет подсчитываться по формуле ∆S=2πR∆R. Поскольку точка безразмерна, ожерелье из них составляющее протяжение 2πR, будет иметь равную длину на внешней и внутренней стороне кольца. Чем больше R, тем больше приращение ∆S, так как при равном увеличении ∆R каждый последующий шаг даёт большее приращение площади, - нелинейность её прироста. Произведение двух линейных величин R⋅∆R это площадь. Значит, для подсчёта всех площадей нам нужна формула их изменения на всём протяжении R. Но 2πR⋅∆R ещё площадь под линейной функцией, с которой мы начали наше исследование интегрирования вида x⋅∆x. Её первообразная парабола, а описываемая формула 2πR2/2=πR2.
Мы можем поставить задачу определения сторон прямоугольного параллелепипеда имеющего при данной площади поверхности S максимальный объём.
(V=a*b*c, S=2ab+2ac+2bc, c=V/ab, откуда S=2ab+2V/b+2V/a. Вычисляем производную и приравниваем к нулю: dS/da=2b-2V/a2; dS/db=2a-2V/ba2; b=V/a2, a=V/b2 откуда V=b3=a3=c3 - получается куб.) Берём формулу площади поверхности и исследуем её при помощи дифференцирования сделав переменной сначала в одном измерении, потом в другом, при стационарном объёме. Тогда третье измерение получается автоматически. Узнав минимум (точку экстремума), в котором функция площади (первообразная) сменяет убывание на возрастание, мы вычисляем все три стороны прямоугольника. Нужно установить в двух измерениях этой функции точки, касательные к которым будут параллельны оси абсцисс, то есть тангенс угла их наклона равен нулю, как и значения производных в этих точках. Приравнивание соответствующих производных к нулю даёт нам искомые точки. Система из трёх уравнений определяет все три переменные. 

Графики площади поверхности и объёма шара, куба, правильного икосаэдра показывают нам непрерывный рост. Минимальное значение они имеют при нулевом значении радиуса. Поэтому все эти фигуры имеют минимальную площадь поверхности при максимальном объёме, какое бы значение радиуса вписанной окружности мы не взяли. Полная центральная их симметрия дифференциально увязывает объём с площадью поверхности.
Уравнение закона свободного падения открытое Галилеем имеет вид h=h0-gt2/2 Оно указывает, какой путь в любой момент времени t пройдёт отпущенное над поверхностью Земли тело при отсутствии сопротивления воздуха. Продифференцируем эту функцию по времени h`=v=-gt и получим функцию, которая показывает скорость тела в любой момент времени t. Ещё раз продифференцируем уже раз продифференцированную функцию и получим h``=v`= a =-g константу ускорения свободного падения на планете Земля.

На графике первообразной параболы тангенс угла наклона касательной к оси абсцисс, в какой либо точке t равен скорости этого тела в это же время. "Святая троица" графиков показывает нам, что каждая последующая производная это скорость предыдущего изменения. В данном случае первая производная - скорость нарастания пройденного пути, а вторая производная - скорость изменения скорости, т.е. ускорение. К дифференцированию прибегают всякий раз, когда встает вопрос о скорости изменения какой-либо функции по мере изменения аргумента, когда эта скорость оказывается непостоянной, а определять ее требуется точно для любого значения аргумента. Возьмём такой случай.

В каждый момент времени движущееся тело имеет строго определённую скорость, говорит нам график зависимости скорости от времени. Но физически за время равное нулю замер скорости сделать невозможно, - такого значения времени не существует. (Ещё древний грек Зенон заметил, что за время равное нулю летящая стрела неподвижно висит в пространстве.) Придётся взять бесконечно-малую долю времени не имеющую физического дления, то есть ∆t, что будет означать на графике уже некоторую невещественную площадь прямоугольника с этим основанием, и высотой V. Соответственно за время ∆t измерения скорости, тело пройдёт не имеющее вещественной длины расстояние ∆s, и на графике зависимости пути от времени это получит своё отражение. (Опять отношение невещественных отрезков даёт вещественную величину.) Отсюда вывод, - функция пути от времени состоит из бесконечно малых участков, каждый из которых имеет свой угол наклона. Отношение ∆s/∆t (тангенс угла наклона в точке t) на этом графике равно скорости V на графике производной (зависимости скорости от времени) в этой же точке t. Таким образом, оси координат первообразной и производной состоят хоть и из безразмерных, но таких же, при бесконечном суммировании обретающих протяжение, обычно неравных друг другу, связанных с крутизной наклона касательной в данной точке ∆, как и исследуемые нами точки функций. В этом смысле все сечения шара, чей объём мы считали выше, тоже содержат в себе безразмерную толщину дольки, которые, бесконечно суммируясь под кривой и дают общую "толщину" всего шара. На самом деле происходит неразрывный перенос всех площадей сечений в площадь под кривой производной. Однако метод позволяет с чудесной лёгкостью выхватывать точки экстремумов, в которых функция меняет знак, определяя минимумы и максимумы.

Бесконечно малое не существует подобно атомному ядру или нейтрону, оно плод нашего воображения, логическая условность, разбивающая на части реальную протяженность. Отождествление площади круга площади прямоугольного треугольника происходит в целом, а обоснование, - через условное разбиение на бесконечно малые сектора с последующим их сложением в изменённом виде.
*      *      *
Разберём, как интегрирование помогло найти формулу закона радиоактивного распада.
Экспериментальным путём установили - за одно и то же время радиоактивных ядер исследуемого нуклида или изотопа становится в два раза меньше. Требуется найти формулу расчёта количества ядер для любого времени t. Если от цикла к циклу за одно и то же время распадается в два раза меньше ядер, равномерно убывает и скорость распада (рис а). Введём свою для каждого нуклида постоянную λ, гарантирующую равенство ∆N/∆t=-λN (знак минус означает убывание количества ядер) бесконечно малого изменения количества ядер за бесконечно малое время. У каждого значения N своё соотношение ∆N/∆t, максимальное при начальном количестве ядер и минимальное при приближении N к нулю на искомой N(t).
Пусть N=200 ядер. За ∆t их становится вдвое меньше, - ∆N=100. Тогда:
Первый цикл: ∆N/∆t=-λN => 100/1=-λ200 => 1/2=-λ
Второй цикл: 50/1=-λ100 => 1/2=-λ
Третий цикл: 25/1=-λ50 => 1/2=-λ
Чтобы решить нашу задачу слева сгруппируем количество ядер, справа время: ∆N/N=-λ∆t. Слева гипербола Y=∆N/N=(1/X)dx (рис б), справа константа Y=-λ∆t=-adx (рис в). Каждому произведению значения гиперболы на ∆N через равенство соответствует произведение константы на ∆t. Элементарная площадь с меняющимися высотой 1/N и шириной ∆N равна элементарной площади с постоянной высотой λ и шириной ∆t.
Сравним приращения площадей справа и слева. Пусть λ=1
При N=0,001, f(N)=1/N=1/0.001=1000; ∆N⋅f(N)=-1⋅∆t => ∆N⋅1000=-∆t => ∆N=-∆t/1000
При N=1, f(N)=1; ∆N⋅f(N)=-1⋅∆t=> ∆N⋅1=-∆t=> ∆N=-∆t
Получается 1000=1
Этого абсурда можно избежать, допустив изменение ширины ∆N в зависимости от положения на координатной прямой (рис б). ∆N в точке N=0,001 в тысячу раз тоньше, чем в точке N=1. Ведь чем больше N, тем больше ∆N (50<->25, 100<->50, 200<->100). ∆N/N произведение бесконечно малого на число, делающее всё произведение тоже бесконечно малым. Если мы теперь переведём всю площадь под первым и вторым графиками в соответствующее протяжение первообразных функций, то сможем в одномерном виде просуммировать элементарные разношёрстные невещественные участки в любых нужных нам границах до вещественных величин.
 Nt              t
∫∆N/N=-∫λ∆t => Ln(Nt/Nо)=-λt => Nt=Nое-λt
Nо             0
Вот так чисто математический метод помог найти формулу с заявленными условиями.
При переходе от равенства производных к равенству первообразных Ln(N)=-λt возникает точное соответствие уже не между бесконечно малыми площадями, но между точками, что даёт возможность введя одно значение получить другое. Площади под кривыми разной формы интегрированием унифицируются, превращаясь в равновеликие точки из которых складываются отрезки первообразных. Причём эти точки рассматриваются уже не в аспекте наклона, - вне размера.

Если теперь мы продифференцируем полученное выражение по времени dN/dt и возьмём результат по модулю, назовём его активностью Nt`= I = λNое-λt, переобозначим так же λNо на Iо, то получим запись производной It=Iое-λt очень похожую на первообразную. На самом же деле производная, она же скорость убывания первоначального количества ядер, опущена и перевёрнута по сравнению с первообразной на – λ. Интегрирование по частям помогло нам преобразовать неясное равенство, из которого выразили количество ядер ("путь" так сказать). Затем продифференцировали его получив скорость распада.

Можно найти функцию убывания во времени числа радиоактивных ядер "на коленке". ∆N/∆t=-λN говорит о равенстве отношения ∆N/∆t некоей функции в любой её точке (наклон касательной) её же значению, а такую функцию мы уже встречали, это экспонента ex. Только вместо x у нас –λx. Тогда первообразная е-λt, а производная -λе-λt. е-λt пересекает отвечающую за количество распадов ось ординат в точке 1. В нулевой момент, когда начинается распад, искомая кривая должна стартовать с первоначального значения количества радиоактивных ядер Nо. Добавляем его в формулу первообразной и производной.

Равенство ∆N/∆t=-λN, где ∆N – распавшиеся ядра, а N нераспавшиеся описывает на графике первообразной уменьшение числа целых ядер по мере продвижения вправо по оси абсцисс, символизирующей время. Это кривая и тех и других ядер, как кривая пути показывает уже пройденный и ещё предстоящий путь сразу. Но в отличии от формулы расчёта пути, отсчёт идёт в обратную сторону, - вычисляется "непройдённый путь". (Расчёт пути "в обратную сторону" мы тоже приводили выше h=h0-gt2/2.) Когда мы задаём t, выше точки Nt по оси ординат кривая обозначает уже распавшиеся ядра. Все точки под Nt ещё целые ядра. Сама точка Nt уже не целая, но и не распавшаяся.

Укажем нюанс между математической и физической вероятностями. Возьмём десять рослых людей и будем откладывать на абсциссе их рост, а на ординате количество людей, попадающих в определённый диапазон, например, рост 195+/-2 см в нашей группе имеют три человека. Эти три человека будут вершиной кривой Гаусса. По краям расположатся более низкие и более высокие группы, составляющие нисходящие и восходящие ветви кривой. Если мы возьмём тысячу случайных людей, кривая Гаусса у нас останется, но станет больше и шире. И чем больше в нашей выборке людей, тем больше кривая, и тем меньше диапазон сложения. Заменим людей на ядра вещества, испытывающего радиоактивный распад, а рост на время жизни отдельного ядра. Всё та же кривая Гаусса. Но когда мы интегральным путём получали математическое описание закона радиоактивного распада мы предполагали бесконечно большое количество распадающегося вещества что даёт нам возможность свести интервал к бесконечно малому и добиться математической точности, которой в реальности нет. То есть если мы говорим о математике, то множество величин роста или времён жизни ядер ведут себя так, словно знают рост или  время жизни всего остального множества, сверяясь с ним, чтобы занять своё место на кривой, а в реальности это всегда конечное множество приближённых из-за ненулевого интервала значений обусловленное неким единым обстоятельством, как например, прибоем формирующим размер гальки.
*      *      *
Есть способ интегрирования, который образно можно сравнить с суммированием попарно разложенных зёрен гречки и риса из двух разных бесконечно больших пакетов. Для решения сложных задач складываются уже эти пары. Формула для расчёта момента импульса материальной точки: L = ω J, где:
• L — момент импульса материальной точки;
• ω — угловая скорость движения материальной точки;
• J = mR2 — момент инерции материальной точки массой m, вращающейся по траектории радиуса R.
Возьмём диск радиуса R, и посчитаем момент его инерции при вращении вокруг центральной оси. Диск состоит из точек, расположенных на переменном радиусе r. Если разделить диск на окружности, то каждая из них будет иметь массу ∆m, образуемую площадью ∆S (при соответствующем значении r и ширине dr), и поверхностной плотностью диска M/πR2. Большие и меньшие радиусы имеют больший или меньший момент инерции элементарного кольца, так как с ростом радиуса растёт плечо, и площадь кольца, а, значит, масса. Это видно из формул.
dm=∆SM/πR2= (2πrM/πR2)dr=(2M/R2)rdr и J=∫r2dm = 2M/R2∫r3dr
При этом шаг dr остаётся постоянным. Сначала элементарная окружность превращается в точку переменной массы dm, к которой прикладывается усилие переменного плеча, потом преобразуется в rdr помноженное на постоянную, потом добавляется множитель r2 момента инерции. На последнем этапе подсчитывается вся площадь под кубической кривой, то есть суммируется бесконечное множество произведений ставшего постоянным размера точки на куб плеча. Диск превратился сначала в точки, потом в линию, потом, став  моментом инерции в площадь, и снова в линию. Мы не можем взять всю площадь диска целиком. Его нужно разъять на бесконечность, перемножить на плечи, и снова сложить обратно в неразрывную материю!

Для подсчёта момента инерции диска при вращении вокруг диаметра, разбивать его следует не по радиусам, а точно так же, как мы разбивали площадь под перевёрнутой параболой, на элементарные столбики, параллельные диаметру вращения. Они будут иметь разную высоту/площадь, и вращаться на разных плечах. Их масса так же "концентрируется" в точки. Переменная dm так же выражается через длину столба, шаг ∆x и поверхностную плотность: ∆S=2√(R2-x2)dx. Как и в предыдущем случае суммируются соответствующие произведения ∆x на значение подынтегральной функции, - элементарная площадь под этой кривой, она же элементарный момент инерции. Только преобразования сложнее. Координатная ось X проходит через центр диска и перпендикулярна оси вращения.

Для подсчёта момента инерции шара при вращении вокруг диаметра, разбиение идёт по слоям/элементарным дискам, напоминая расчёт объёма шара. Суммируется момент инерции каждого такого элементарного диска, формула расчёта которого была получена ранее. Переменная интегрирования x – расстояние от центра шара до центра элементарного диска перпендикулярного оси вращения, ∆x – толщина элементарного диска. Тут мы тоже переводим бесконечно малую массу элементарного диска, в бесконечно малые линейные размеры. Если её записать через радиус и плотность (уже объёмную) dJ=mr2/2=ρπr2dx⋅r2/2, а переменную радиуса через отрезок (координату) (r2=R2-x2), то бесконечно малым у нас будет только ∆x, по которому мы и интегрируем. Сначала взятие формулы расчёта момента инерции для диска, потом подстановка в неё вместо массы функции описывающей изменение массы элементарного среза через координату, и суммирование моментов инерции всех таких срезов, - превращение в отрезок первообразной.

Интегрирование работает даже, когда разъятые на бесконечное множество какие-либо элементы как угодно вступают во взаимодействие с другими бесконечными элементами. В этом случае мы перестаём пытаться представлять их конкретными физическими процессами, но просто функциями подобно преобразованиям многочленов. Важно только чтобы каждой элементарной площади под кривой производной соответствовал свой размер точки первообразной, и никаких лишних точек или площадей не было. И мы всегда можем свести элементарную трапецию под кривой к строго прямоугольному виду, как показано в начале этой статьи, распрямляя кольца, или любые другие правильные фигуры.   

Сделаем самое широкое обобщение.

Мы представляем состоящую из бесконечно малых декартову систему координат, образы функций изучаемых процессов, а также наше представление об бесконечно малом, и с бесконечной скоростью множащемся бесконечно большом. Одномерные, то есть бесконечно малые объекты, мы приравниваем к двумерным, двумерные к трехмерным, и наоборот. Мы ставим в точном соответствии бесконечное множество точек бесконечному множеству отрезков, из которых слагается площадь. Мы не можем для проверки своей версии тонко и изящно нарисовать график функции, чтобы при помощи мощного микроскопа увеличив его, увидеть изломы прямых участков, из которых такая кривая состоит. Мы только мыслим себе это. Интегрально-дифференциальное чудо стало возможным благодаря двум перекрещивающимся бесконечностям, - бесконечно мелкому разбиению и бесконечно большому их сложению. Оно поймало непрерывное, постоянное, бесконечно быстрое движение в настоящий момент в окружающем нас мире.

Очевидно, что использование интегрально-дифференциального метода показывает нам ложность разделения математического мира на качество-количество, и единство-множественность. Отказ от противопоставления распахивает бескрайние горизонты возможностей. Для того, чтобы он работал, нам нужно принять мир, в котором количество нулей без границ между ними, без линейных размеров имеет строго определённое направление в пространстве, и мгновенно, непрерывно, вечно перетекает в качество протяжения. Мы обязаны думать, что процесс бесконечно быстрого размножения бесконечно малых не прерывается никогда. Точка не имеет протяжения, имея чёткую ориентацию в пространстве. Вещественный отрезок состоит из бесконечного множества непротяженных точек. "Находясь" на бесконечно-малой точке мы не можем перейти на соседнюю, так как не можем её "увидеть", и тем ни менее наша точка являющаяся неделимой единицей касания касательной состоит из отрезков в системе координат ∆X и ∆Y имеющих два конца каждый, и обладающих вследствие этого бесконечным множеством точек между собой. Но в этом конкретном случае мы должны допустить, что между концами отрезков нет точек, а самих концов - один у каждого отрезка.

Раз качество и количество, единство и множественность не противоположны друг другу, поскольку противопоставление не соответствует реальности, говорит математика, то привычное представление пространства тоже ложная идея. А это значит, что и неразрывно связанная с пространством идея времени, к которой мы привыкли с детства, так же ошибочная концепция. Если бесконечно просуммировать ничто, появится пространство и время. Если его бесконечно не суммировать, то на преодоление в отдельности каждого бесконечно малого не нужно реального времени. Пространство и время берутся из ничего, и в ничего исчезают! Кто-то скажет, что это ведь только свойство математического, а не реального мира, но рассчитываем-то мы при помощи математики для реального мира, и, значит, математический мир составная его часть.

Использование интегрально-дифференциального исчисления позволяет нам сделать вывод теоретической физики глобальной важности.

Согласно механике Ньютона скорость: v=dx/dt, импульс: p=m*dx/dt=mv, сила F=dp/dt=m*d2x/dt2=m*dv/dt, работа/энергия: dA=F*dx=(m*d2x/dt2)vdt=(m*dv/dt)vdt=mvd2x/dt= mvdv
v - абсцисса, A - ордината. Чтобы узнать всю работу/энергию А/Е при v от нуля до бесконечности, интегрируем выражение mvdv, то есть считаем площадь под этой прямой. Получаем Е=mv2/2 - кинетическую энергию.

Как увеличивается импульс от точки к точке, если в каждой конкретной точке он неизменен? Предположим, что в точке 1 импульс неизменен, а перескочив в соседнюю уже изменился. Тогда получится, что длина абсциссы v состоит из промежутков между точками, в которых импульс неизменен, что очевидный абсурд. Либо между точкой, в которой импульс неизменен и той, в которой он уже изменился мы можем вставить бесконечное множество точек, а между ними ещё, и никогда не сдвинемся с места, не изменим импульс. Значит, при изменении импульса скорость должна меняться уже в каждой точке "на её протяжении". Отсюда все эти ∆E/∆v, ∆Q/∆T, dx/dt, dv/dt, - берём среднее по бесконечно малому отрезку и делим его на такое же среднее.

На скоростной шкале v импульс в точке равен mv. Но каждая точка v имеет ширину (толщину) ∆v означающую прирост импульса в масштабе одной точки. Этот прирост требует выделения/потребления энергии ∆E. Таким образом произведение импульса в точке mv на ширину этой точки mv∆v=∆E и потому площадь под кривой импульса будет равна необходимой для этого импульса энергии. Так как ∆v постоянна, рост площади будет определять крутизна роста функции mv.

Из опыта Майкельсона-Морли и преобразований Лоренца известно, что часы движущейся системы замедляются в сравнении с часами неподвижной системы на произведение фактора Лоренца √(1-v2/c2) При приближении скорости движения к световой, это выражение, становясь всё меньше, убывает до нуля, тяня в ноль сомножители. Если же оно располагается в знаменателе, то оно точно так же до бесконечности увеличивает любое число. Релятивистское переписывание формулы для импульса внесёт фактор Лоренца как раз в знаменатель. Посчитаем релятивистское выражение для полной энергии тела имеющего массу покоя.


Интегрально-дифференциальный метод позволил нам открыть удивительную тайну природы - любая масса сама по себе является энергией невероятной мощности! При скорости равной нулю полная энергия тела массой m равна mc2.

Поливанов О.И.
19.05.2021г

Share on Facebook! Share on Twitter! g+ Reddit Digg this story! Del.icio.us StumbleUpon

Статьи в « О. Поливанов »

Комментарии *