Задача.
На космической станции с искусственной гравитацией поднимают (опускают) груз со скоростью \(V_0 = 1~м/c\).
Радиус от центра вращения до потолка технического блока \(r_0 = 50~м\).
Лебёдка закреплена на потолке.
Груз движется в поле сил инерции и на него действует сила реакции со стороны троса.
Найти статический угол отклонения троса от вертикали.
Записать закон сохранения энергии с учётом вращения корабля.
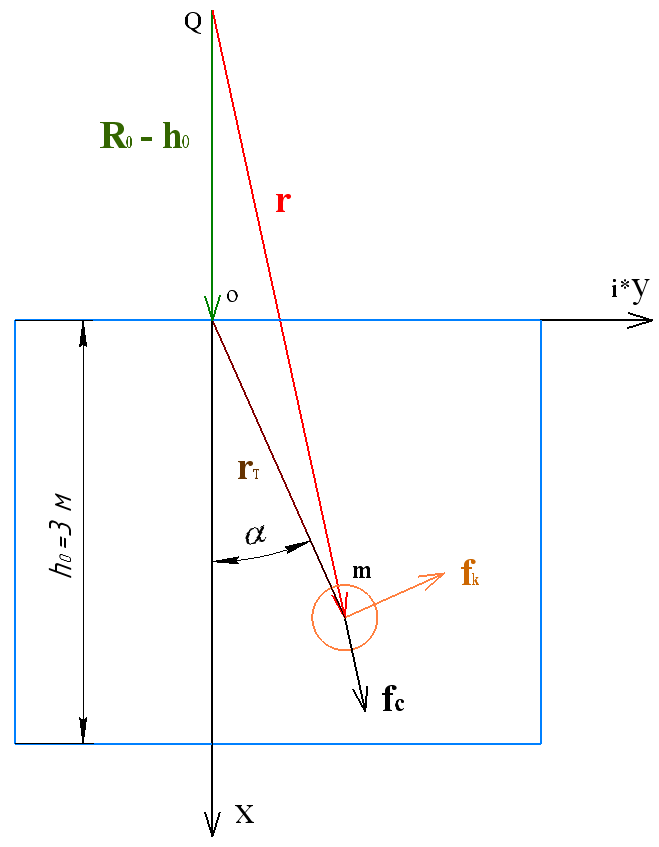
Уравнение движения груза можно записать так
\(\displaystyle m~ \vec a =\vec f -2m \left[\vec \Omega_z \times \vec v \right] + m~Ω_z^2~ \vec r\), где
\(\vec f~-\) сила реакции со стороны троса.
Для упрощения уравнения сделаем следующее пояснение.
Пусть единичный вектор
\(\vec q\) проходит вдоль длины троса, а единичный вектор
\(\vec Q\) перпендикулярен тросу, тогда
имеет место следующее уравнение
\(\vec Q \cdot (\vec Q \cdot \vec a_{~'}) = -\vec q \cdot (\vec q \cdot \vec a_{~'})+ \vec a_{~'}\).
(1)Умножаем скалярно на вектор \(\vec Q\)
\( (\vec Q \cdot \vec Q) \cdot (\vec Q \cdot \vec a_{~'}) = -(\vec Q \cdot \vec q) \cdot (\vec q \cdot \vec a_{~'})+ \vec Q \cdot \vec a_{~'}\).
\( (\vec Q \cdot \vec a_{~'}) = \vec Q \cdot \vec a_{~'}\), так как
\(\vec Q \cdot \vec Q =1\), а
\(\vec Q \cdot \vec q = 0\).
Умножаем скалярно на вектор \(\vec q\)
\( (\vec q \cdot \vec Q) \cdot (\vec Q \cdot \vec a_{~'}) = -(\vec q \cdot \vec q) \cdot (\vec q \cdot \vec a_{~'})+ \vec q \cdot \vec a_{~'}\).
\( - (\vec q \cdot \vec a_{~'})+ \vec q \cdot \vec a_{~'}= 0\), так как
\(\vec q \cdot \vec q =1\), а
\(\vec Q \cdot \vec q = 0\).
Получили равенство для двух линейно независимых направлений.
Можно сказать, что вектор
\( \vec a_{'}\) является суммой двух ортогональных векторов с длинной равной
проекциям вектора
\( \vec a_{'}\) на направления
\(\vec q\) и
\(\vec Q\).
\(\vec Q \cdot (\vec Q \cdot \vec a_{~'}) +\vec q \cdot (\vec q \cdot \vec a_{~'}) = \vec a_{~'}\).