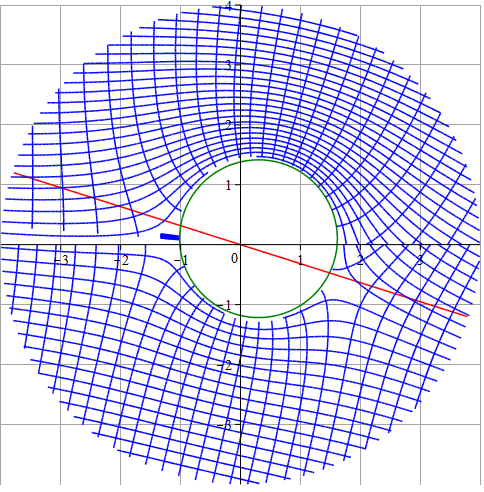
Рассмотрим теорию обтекания цилиндра потенциальным потоком и применим к теории крыла
через конформное преобразование Жуковского
\(\displaystyle z=\frac{1}{2}\left(\zeta+\frac{a^2}{\zeta}\right)\) \((1)\) .
Эта функция комплексного переменного. Она отображает окружность на профиль крыла.
Форма профиля зависит от параметров окружности.
Обозначим координаты центра окружности на комплексной плоскости
\(\zeta\) как
\(\mu=\Delta x+ i~\Delta y\).
Тогда радиус окружности можно записать, так
\(R=a+|\mu|\).
Координаты окружности
\(\zeta (\theta)=R~(cos(\theta) + i~sin(\theta))+\mu = R~e^{i~\theta}+ \mu\).
Например, пусть
\(a=1\); \(\Delta x=0.3\); \(\Delta y=0.1\); \(R=1.3162\).Тогда функция
\(\displaystyle z(\theta)=\frac{1}{2}\left(\zeta(\theta)+\frac{a^2}{\zeta(\theta)}\right)\) нарисует такой профиль
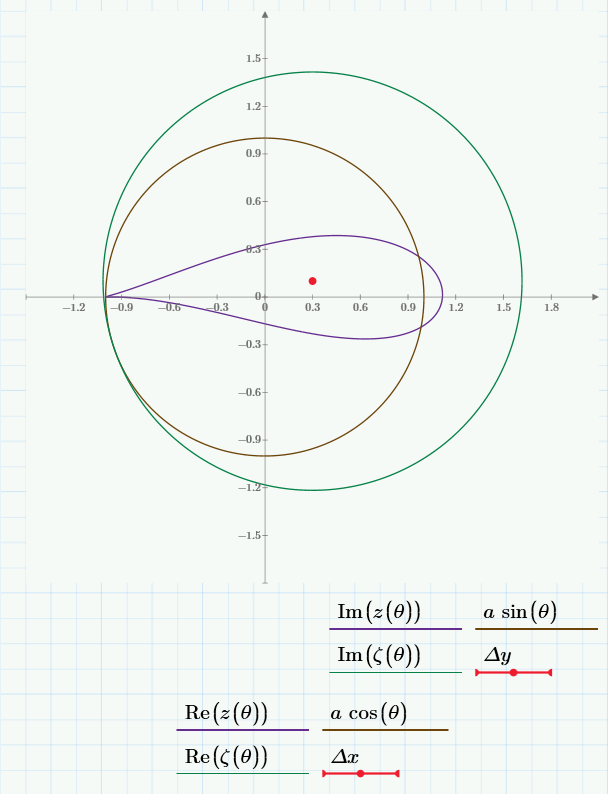
Хорда профиля в проекции на ось
\(x\) равна
\(b=2.1163\). Проекция и хорда практически равны.
Комплексный потенциал течения вокруг круга, расположенного в центре системы координат.\(\displaystyle f(\zeta)=-V_0 \left(\zeta+\frac{R^2}{\zeta}\right)-\frac{i~\Gamma}{2 \pi}~ln(\zeta)\) \((2)\), где
\(V_0~-\) скорость потока;
\(\Gamma~-\) циркуляция вокруг круга.
Переходим в систему координат с углом атаки \(\alpha\) и смещением
\(\mu\);
\(\displaystyle \zeta=(\zeta_1-\mu)~e^{i~\alpha}\).
В этой системе координат потенциал
\((2)\) с точностью до постоянной запишется так
\(\displaystyle f(\zeta)=-V_0 \left(\zeta~e^{i~\alpha}+\frac{R^2~e^{-i~\alpha}}{\zeta-\mu}\right)-\frac{i~\Gamma}{2 \pi}~ln(\zeta-\mu)\).
Произвольная постоянная не влияет на построение линий тока и дифференцирование потенциала.
В полярной системе координат
\(\displaystyle f(r,\theta)=-V_0 \left(r~e^{i~\theta}~e^{i~\alpha}+\frac{R^2~e^{-i~\alpha}}{r~e^{i~\theta}-\mu}\right)-\frac{i~\Gamma}{2 \pi}~ln(r~e^{i~\theta}-\mu)\).
Строим линии тока при
\(V_0=1\) и
\(\Gamma(\alpha)=5\); \(\alpha= 13.197^\circ\).