Я доказал правоту Ферма
Уравнение Ферма имеет следующий вид
А^3 + B^3 = C^3
Это значит, что Ферма говорил, что нельзя добавить к кубу другой целый куб и получить новый целый куб, где С целое число.
Потому задачу решать надо построением нового куба, а не разложением бинома на всякие ряды на ста страницах.
Ферма говорил, что решение простое.
Это значит, что к исходному Куб (А^3) надо достроить из кубиков меньшего Куба (B^3) и получить целый куб (С^3).
Отсюда получается дополнительное условие, которые не замечали предыдущие решатели.
При построении нового куба сторона нового куба должна увеличится на 2 слоя. Станет (А+2)
Если добавить еще два слоя, то сторона станет (А+4) и количество добавляемых кубиков станет больше исходного куба.
Берем куб со стороной 10 кубиков.
(10+4)^3 -10^3 = 2744-1000 = 1744 > 1000
Потому можно рассматривать только добавление одного слоя, что я и делаю.
Куб суммы раскладывается так
(a+cool.gif^3]=a^3+3ba^2+3ab^2 +b^3
Из условия задачи количество добавленных кубиков должны образовать целый куб.
(A + 2)^3 – A^3 = А^3 + 6А^2 + 12А + 8 – А^3 = 6А^2 + 12А + 8 = Х^3
Квадратное уравнение вида
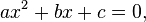
имеет решение

a = 6, b = 12, C = (8 – Х^3)
b^2 = 144
b^2 - 4ac = = 144 – 192 + 24Х^3 = 24Х^3 – 48 = 24(Х^3 -2)
√24(Х^3-2) = √24*√(Х^3 -2)
√24 = 4,8989794855663561963945681494118.. число иррациональное. Значит и А число иррациональное. А должно быть целым.
Следовательно условие сложения кубов Ферма не выполняется.
Значит нельзя сложить два куба в целый куб и теорема Ферма доказана..
А остальное , только питицеольство
С чем я вам и привет