Вы сейчас, похоже, даже не понимаете, про что говорите. Двойной безнейтринный бета-распад связан с майорановской массой нейтрино ровно так же, как и Ваша схема с посоедовательными процессами.
Напротив, это просто вы так и не поняли, что я "своей схемой": \[1)~~n\to p+e^-+\overline{\nu}\\ 2)\begin{cases} \overline{\nu} \to \nu~~\text{(вариант №1)}\\ \nu\equiv \overline{\nu} ~~\text{(вариант №2)} \end{cases} \\3)~~ n+\nu\to p+e^-\]…описал "детали" ситуации, приводящей (в конечном счете) к веселой картинке, именуемой диаграммой Фейнмана:
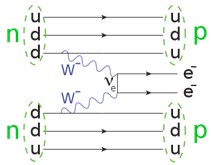
…которая, ничего реально не объясняет, а только констатирует желание "видеть" двойной безнейтринный бета-распад. Вне зависимости от того, есть ли этот распад в действительности или его – нет.
Так вот, еще раз о том же самом.
Моя схема наглядно показывает, что для реализации того, что изображено на картинке Фейнмана, необходим факт совершения обмена нейтрино между двумя нейтронами. Условием этого обмена ("вторая реакция" схемы) является выполнение одного из двух вариантов (других не вижу) "поведения" нейтрино: либо осцилляция, либо "майоранизация" этой частицы.
Но, главное, что, при этом, двойной бета-распад должен (просто ОБЯЗАН) сопутствовать "одинарному", в случае "нежелания" нейтрино взаимодействовать со вторым нейтроном (отсутствие "третьей реакции" схемы). Чего на веселой картинке Фейнмана, разумеется, никак не разглядеть. И чего (невзирая на всю "неописюемую красоту" картинки Фейнмана), в реальности просто НЕТ, по причине (на основании закона сохранения энергии) антагонизма двойного и одинарного бета-распадов.
Так, если у вас нуклон распадается по каналу двойного (безусловно нейтринного) распада, то он (этот самый нуклон) уже никак НЕ может распадаться по одиночному каналу. Типа: \[~^{116}_{~48}Cd\to ~^{116}_{~50}Sn+\beta +\beta \\~^{116}_{~48}Cd\not\to ~^{116}_{~49}In+\beta \]И получаемое, таким образом, противоречие является "доказательством от противного" полной дебильности (абсолютной оторванности от какой-либо реальности – мягче выражаясь) диаграммы Фейнмана.