Луна замедляет вращение Земли

[Мастеров АВ]

Часть энергии вращения Земли передаётся Луне,
из-за чего Земля замедляет своё вращение,
а Луна удаляется от Земли на 38 мм в год.
(а остальная часть энергии вращения Земли
тратится на разогрев мантии,
движение континентов, приливы,
вулканическую активность и
землетрясения)

ВОПРОС: На сколько секунд земные сутки
станут длиннее за 1000 лет?

Давайте будем посчитать:

Будем использовать закон сохранения момента импульса.
Т.е., суммарный момент количества движения (вращения) Луны и Земли
должны сохраняться.

Для Луны (как для точечного тела) момент инерции: \(J_m=mL^2=1.1\ 10^{40}кг\dot{} м^2\)
\(m\) - масса Луны
\(L\) - расстояние до Луны



Если бы Земля была шаром,
плотность материи в котором
по всему объёму одинакова, то
момент инерции шара:

\(J=\frac{2}{5}MR^2\)

Но плотность земли в ядре
существенно больше, а потому
момент инерции Земли меньше,
чем у шара:

\(J_e=0.335\ MR^2=3.746\ 10^{37}кг\dot{}м^2\)

Угловая скорость вращения Земли:
\(\omega_e=\frac{1}{24\dot{}60\dot{}60}=1.16\dot{}10^{-5}\ c^{-1}\)

Угловая скорость вращения Луны вокруг Земли:
\(\omega_m=3.9\dot{}10^{-7}\ c^{-1}\)

Суммарный момент импульса:
\(J_e\omega_e+J_m\omega_m=4.35\dot{}10^{32}+4.3\dot{}10^{33}=4.7\dot{}10^{33}кг\dot{}м^2\dot{}c^{-1}\)
и это значение должно сохраняться.
========================

С Изменением расстояния до Луны,
меняется её период обращения
(угловая скорость).

Т.е., в нашей задаче переменными являются
все параметры в этом выражении (кроме \(J_e\)):

\(J_e\omega_e+J_m\omega_m\)

но эта сумма остаётся постоянной. Т.е.:

\(J_e\frac{d\omega_e}{dt}+\frac{dJ_m}{dt}\omega_m+J_m\frac{d\omega_m}{dt}=0\)

\(J_e\frac{\Delta\omega_e}{\Delta L}+\frac{\Delta J_m}{\Delta L}\omega_m+J_m\frac{\Delta\omega_m}{\Delta L}=0\)

\(\Delta L=38\) мм в год
\(\frac{\Delta L}{L}=10^{-10}\)

При этом известно, что период обращения (Луны) вокруг Земли
связан с расстоянием до луны так:

\(-\frac{\Delta \omega_m}{\omega_m}=\frac{\Delta T}{T}=\frac{3}{2}\frac{\Delta L}{L}=\frac{3}{2}\frac{0.038}{3.844\dot{}10^{8}}=1.5\dot{}10^{-10}\) в год

\(\frac{\Delta \omega_m}{\Delta L}=-\frac{3}{2}\frac{\omega_m}{L}\)

\(\frac{\Delta J_m}{J_m}=2\frac{\Delta L}{L}\); \(\frac{\Delta J_m}{\Delta L}=2\frac{J_m}{L}\)

\(J_e\frac{\Delta\omega_e}{\Delta L}+2\frac{J_m}{L}\omega_m-J_m\frac{3}{2}\frac{\omega_m}{L}=0\)

\(J_e\frac{\Delta\omega_e}{\Delta L}+J_m\frac{1}{2}\frac{\omega_m}{L}=0\)

\(\frac{\Delta\omega_e}{\omega_e}=-\frac{J_m}{J_e}\frac{1}{2}\frac{\Delta L}{L}\frac{\omega_m}{\omega_e}\)

\(\frac{\Delta T_e}{T_e}=\frac{1}{2}\frac{J_m}{J_e}\frac{\omega_m}{\omega_e}\frac{\Delta L}{L}\) - замедление времени вращения Земли (в относительных величинах)

\(\Delta T_e=\frac{1}{2}\frac{J_m}{J_e}\frac{\omega_m}{\omega_e}\frac{\Delta L}{L}T_e\) - замедление времени вращения Земли (в абсолютных величинах)

\(\Delta T_e=\frac{1}{2}\frac{mL^2}{0.335\ MR^2}\frac{24}{709}10^{-10}86400\)

\(\Delta T_e=\frac{1}{2}\frac{1}{0.335}\frac{m}{M}\frac{L}{R}^2\frac{24}{709}10^{-10}86400\)

\(\Delta T_e=\frac{1}{2}\frac{1}{0.335}\frac{1}{81}\left(\frac{384400}{6371}\right)^2\frac{24}{709}10^{-10}86400=2\dot{}10^{-5}\)

\(\Delta T_e=0.02\) - за тысячу лет сутки стали длинее на две сотых секунды
\(\Delta T_e=0.04\) - со времён Христа сутки удлинились на четыре сотых секунды

Со времён Христа Луна стала от нас дальше на 76 метров.
Миллион лет назад Луна была ближе к нам на 38 км,
а сутки были короче на 20 секунды.

Десять миллионов лет назад: 380 км и три часа.

[Evalmer]

Луна замедляет вращение Земли...

...и Солнце - тоже.

[Е.А.Меркулов]

Замедление вращения вокру собственной оси грозит от Солнца, разве что Меркурию.
Систему же Земля – Луна ждет "светлое" будущее системы Плутон – Харон.

[Е.А.Меркулов]

останемся нищими в России,
нищими в самой богатой стране

Это все потому, что, по вашей нелепой логике, самые богатые люди должны жить в самой нищей на свете стране.
Я имею в виду такую нищую страну как Япония, в недрах которой нет ни нефти, ни газа, ни золота, вообще ничего нет, окромя землетрясений.

[Evalmer]

Систему же Земля – Луна ждет "светлое" будущее системы Плутон – Харон.

А саму систему Плутон – Харон ждет еще более «светлое» будущее.

[Е.А.Меркулов]

Это вы о чем?

[Артур Васильев]

Часть энергии вращения Земли передаётся Луне,
из-за чего Земля замедляет своё вращение,
а Луна удаляется от Земли на 38 мм в год.
(а остальная часть энергии вращения Земли
тратится на разогрев мантии,
движение континентов, приливы,
вулканическую активность и
землетрясения)

ВОПРОС: На сколько секунд земные сутки
станут длиннее за 1000 лет?

вики дает удлинение за 100 лет на ~ 2 миллисекунды
значит за 1000 лет получаем 0,02 секунды

что касаемо вашего расчета
вы игнорируете что Луна вращается не вокруг Земли, а вокруг центра масс системы "Земля-Луна" - как и Земля
это не просто сложная задача, это очень сложная задача даже для докторов физмат наук - даже для упрощенного кругового экваториального движения / пример
https://www.gemp.ru/article/232.html

в любом случае - вращательный момент в данном случае передается не по формуле, а за счет возникновения двух пар сил: прямой и обратный прилив + прямой и обратный отлив - с учетом вращения Земли вокруг своей оси и вращения Земли и Луны вокруг их центра масс

[Артур Васильев]

вращательный момент в данном случае передается не по формуле, а за счет возникновения двух пар сил: прямой и обратный прилив + прямой и обратный отлив - с учетом вращения Земли вокруг своей оси и вращения Земли и Луны вокруг их центра масс

эта сложность не позволяет увидеть принципиальную картину сил и поэтому делается ставка на уже имеющееся мнение: есть видимое лунное ускорение

тем не менее картина сил простая
по ссылке дана картинка



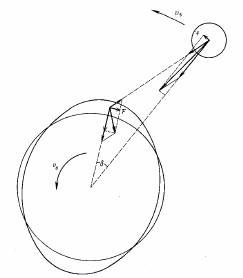
здесь δ - угол отклонения приливного пула от нормали между центрами Земли и Луны
академическая наука уверяет что этот угол равен примерно 2 градусам
при этом Луна далеко, поэтому от Луны отклонение от нормали на приливной пул составит примерно 0,5 градусов

лунное ускорение вызывается как бы силой f - которая на самом деле является проекцией (тангенциальной) реальной силы на касательную к орбите Луны

а эта реальная получается складыванием избытка притяжения к ближнему приливному горбу с недостатком притяжения к дальнему горбу (здесь для Луны отклонение от нормали на дальний приливной пул составит тоже ~ 0,5 градусов)

эти избыток и недостаток системные - так как чуточку растягивается вся Земля
при этом суша приподнимается в среднем ~ на 30 см, а океан ~ на 50 см по отношению к суше

забавно что автор рисунка - доктор физико-математических наук Олег Сорохтин - нарисовал вектор 0,5 градусов на ближний приливной горб и нарисовал обе проекции избытка притяжения: и тангенциальную f и нормальную

но не заметил - ибо нельзя!!!! - что нормальная проекция приливного избытка явно больше тангенциальной, то есть в целом вектор реальной силы направлен явно внутрь лунной орбиты и ДОЛЖЕН - в полном согласии с законом всемирного притяжения - двигать Луну внутрь ее орбиты, то есть сближать с Землей

при угле 0,5 градусов нормальная проекция ~ в 120 раз больше тангенциальной

при этом автор, как и вся научная его братия (в том числе википедии), ограничился верхним приливом

я же проиллюстрировал разницу в своем расчете и соответствующем рисунке
https://pro3001.narod.ru/marx/luna_priliv_img/luna_priliv.htm



а сейчас давайте учтем и обратный прилив
сложим избыток и недостаток
длина вектора недостатка на 6,4% меньше вектора избытка
при этом вектор недостатка направлен как бы противоположно вектору избытка
с отклонением в 1 градус

по теореме косинусов получаем величину реального вектора силы ~ 0,066 от величины вектора избытка на ближний горб
по теореме синусов (+0,5) получаем угол реального вектора с лунно-земной нормалью в 14 градусов

итак
величина результирующего вектора уменьшилась в 15 раз по сравнению с вектором на ближний горб
он повернулся к нормали до 14 градусов
но все так же - как пионер - приветствует закон всемирного притяжения

[Артур Васильев]

14 градусов - это соотношение нормали к тангенциали 4:1

а как же торможение Земли?

никак

в 1952 году перешли на эфемеридное время
в 1960 году начали поверять время атомными часами
и торможение Земли закончилось

https://elementy.ru/nauchno-populyarnaya_biblioteka/436151/Pochemu_Zemlya_vrashchaetsya_neravnomerno_i_kak_eto_vliyaet_na_schet_vremeni

[Ost]

http://bolshoyforum.com/forum/index.php?topic=620522.msg10587915#msg10587915
http://bolshoyforum.com/forum/index.php?topic=620522.msg10587589#msg10587589
http://bolshoyforum.com/forum/index.php?topic=620522.msg10585638#msg10585638

[Evalmer]

Мощность дрейфа Луны \(\displaystyle P_{dl}=-m_l \frac{E_0}{r_0} v_{dl}\).

Это всё – хорошо, но совершенно непонятно, когда (на каком удалении Луны) будет достигнута полная синхронизация (по типу Плутон – Харон) в системе Земля – Луна.
 
И попутный вопрос: оператор « \displaystyle » в Вашей формуле, предназначен только для дробей?

[Артур Васильев]

вращательный момент в данном случае передается не по формуле, а за счет возникновения двух пар сил: прямой и обратный прилив + прямой и обратный отлив - с учетом вращения Земли вокруг своей оси и вращения Земли и Луны вокруг их центра масс

плюс вопросы

• кто/что запрещает-мешает учитывать нормальную проекцию приливной силы, воздействующей на Луну?

• почему в последние 70 лет Луна удаляется, а Земля ускоряется?

• почему геофизики по котидальным картам (суммируя все локальные разные приливы) получают приливную силу на 40% меньшую чем астрономы?
https://geocartography.ru/sites/default/files/sgugit/article_pdf/2018.1.40-53.pdf

Формулы можно использовать разные. В небесной механике, начиная с Эйлера-Лагранжа-Лапласа, используют теорию возмущений с разложениями в ряды различного характера. А геофизики предпочитают считать так:
Рускол Е.Л. Происхождение Луны М., «Наука», 1975 (глава 2)
https://disk.yandex.ru/i/xQoIaVakoGiPRw

Я же понимаю сложность расчета торможения Земли как сложность учета центра тяжести системы "Земля-Луна". Поэтому не лезу туда, ограничиваясь фиксацией приливного воздействия на Луну = 4:1 нормальное и касательное ускорения, то есть точно внутрь орбиты - поближе к Земле. В полном согласии с законом всемирного притяжения: пыль слипается в звезды и планеты, звезды стремятся к ближним звездам, планеты стремятся к ближним звездам, спутники стремятся к ближним планетам.

А если вы лезете, то учитывайте центр тяжести/барицентр системы. Именно вокруг него сбалансированы движение приливных горбов, их смещения и соответствующие дополнительные силы.

В торможении вращения Земли мне достаточно спутниковых наблюдений. В остальном могу лишь заметить, что в моей гравиэфирной модели новая материя накапливается именно в центре земного ядра - равномерно со всех сторон, поэтому Земля в целом должна замедлять свое вращение + Луна должна отдаляться за счет переизлученного Землей гравиэфира (как и Земля от Луны).

При этом планеты порождаются звездами (тайна второго орбитального фокуса). Здесь можно отметить обилие железа и кислорода внутри Земли и задаться вопросом "откуда их столько взялось в межзвездной пыли?"

[Артур Васильев]

История векового ускорения Луны.

Бронштэн В.А. Как движется Луна - 1990 (с.110-116)
https://disk.yandex.ru/d/kbZMKvdHOHS8CA

1. Астрономические наблюдения 18 века обнаружили вековое ускорение Луны ~ на 10" по сравнению с законом всемирного притяжения. Это означало, что орбита Луны постепенно уменьшается и она может упасть на Землю. В 1770 г. Парижская академия наук объявила конкурс на лучшее объяснение этого явления.

2. Сомнения разрешил Лаплас, показавший в 1783 году, что возмущения со стороны планет приводят к изменению эксцентриситета орбиты Земли с основным периодом порядка 24 000 лет. В масштабе 100 лет - это проявляется как видимое с Земли ускорение Луны. Лаплас использовал метод вариации произвольных постоянных Лагранжа (в том числе понятия силовой и возмущающей функций / не путать с понятием энергии, которое сформировалось в 1820-1850 годах).

3. В 1853 году Джон Адамс обнаружил ошибку в расчетах Лапласа и уточнил, что вековое ускорение Луны в его решении составляет примерно 6" в столетие. Шарль Делоне подтвердил расчеты Адамса и в 1865 году предложил объяснить разницу с астрономическими наблюдениями приливными силами, тормозящими вращение Земли. Первым это сделал Джордж Дарвин.

4. Сегодня ученые оценивают видимое с Земли вековое ускорение Луны (ее долготы по эклиптике) как сумму нескольких сил:
а) гравитационное изменение эксцентриситета Земли ~ 6",
б) приливное торможение Земли ~ 15" (на Земле астрономически не замечаемое),
в) приливное ускорение Луны ~ 5"

5. В нынешней википедии пишут, что в реальности (со стороны) это выглядит как замедление движения Луны вокруг Земли на 26" в столетие. При этом Луна удаляется под действием приливного ускорения, переходит на более длинную орбиту и поэтому замедляется на 5" в столетие. В общем: чем безумнее, тем истиннее. Аж слезы радости навертываются...

[VPD]

Это всё – хорошо, но совершенно непонятно, когда (на каком удалении Луны) будет достигнута полная синхронизация (по типу Плутон – Харон) в системе Земля – Луна.
 ...

   Похоже - никогда.
  Раньше Солнце, расширяясь, поглотит Землю ...
https://yandex.ru/q/over_the_moon/11745487873/

[Evalmer]

  Похоже - никогда.

Похоже – это не ответ.
Скорее – ничем необоснованный домысел.

[VPD]

Похоже – это не ответ.
Скорее – ничем необоснованный домысел.

  У автора есть  расчёт, а у вас - лишь  старческое брюзжание.