Жаль, я пока так и не увидел формулы для Ю.а.е например. Что ж может быть, как нибудь, сподоблюсь взять полбанки (или накачаюсь инсулином) и вывести эту формулу. Сдаётся мне, что это совсем не сложно. Но без подпитки не могу боль мень длинно и чётко мыслить. Мысли как в тумане.Сахар за 15 зашкаливает.
Очень боюсь, что вы её не увидите.
Я же говорю, что гипотетическим юпитерианцам надо освящать число 4.
С удовольствием прочту про Ваше понимание этой бесконечности. Или мы об одном и том же или один из нас ошибается (вероятнее всего я). Двух истин не может быть. )<
Моё представление базируется на формировании волн от не точечного источника, колеблющегося поперёк распространения волны
Оно простое. Давайте изменим шкалу декартовой системы координат так, чтобы +oo (плюс бесконечность) переместилась туда, где обычно присутствует 2 (двойка). Можно так сделать, как вы думаете?
Тогда очень интересно будут выглядеть привычные нам со школьной скамейки графики элементарных функций.
Ну, скажем, таких, как: парабола, гипербола...
Помните, как парабола рисуется? y=x
2Вот смотрите параболу в такой системе координат.
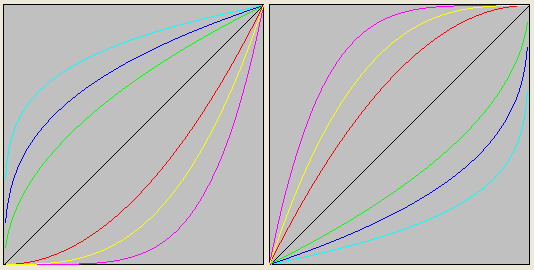
Здесь я оставил только два квадрата из 1-й четверти декартовой системы координат, положительной его части. Всего их 4. Я взял квадраты от 0 до 1 и от 1 до +бесконечности.
Красным цветом изображена привычная нам парабола
y=x2. А синим -- функция
y=x1/2Если рассматривать последовательность
-oo, 0, 1, 2, 3, 4 ...
именно в таком свете, то минус бесконечность здесь очень логична.
